林鴻金,陳省江

(1.福建師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,福建福州 350117；2.寧德師范學(xué)院數(shù)理學(xué)院,福建寧德 352100)

1 引言及主要結(jié)果

假設(shè)讀者已經(jīng)熟知了Nevanlinna值分布理論和Nevanlinna差分模擬理論中的基本理論和符號(hào)[1-2],例如N(r,f),m(r,f),T(r,f)等.

通常所說(shuō)的亞純函數(shù)指的是在整個(gè)復(fù)平面上亞純.如果說(shuō)f(z)和g(z)為亞純函數(shù),a∈C?{∞}為任一復(fù)數(shù).若f(z) -a和g(z) -a的零點(diǎn)相同且每個(gè)零點(diǎn)的重級(jí)也相同,則稱f(z)和g(z)CM 分擔(dān)a.若f(z) -a和g(z) -a有相同的零點(diǎn)(不計(jì)重?cái)?shù)),則稱f(z)和g(z) IM分擔(dān)a.

設(shè)f為復(fù)平面上的亞純函數(shù).對(duì)于任意的非常數(shù)亞純函數(shù)f(z),S(r,f)=o{T(r,f)},r→∞,可能需除去一個(gè)對(duì)數(shù)測(cè)度為有限的例外值.亞純函數(shù)f(z)的級(jí)和超級(jí)分別為

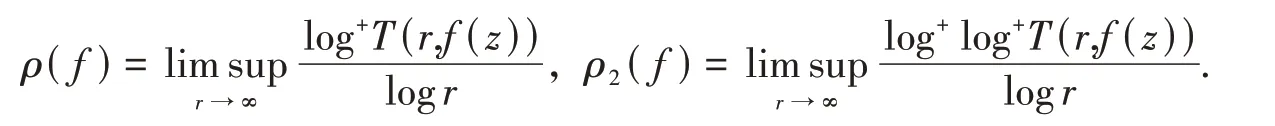
亞純函數(shù)f(z)的一階差分及其n階差分定義如下:設(shè)c為非零復(fù)常數(shù)使得f(z+c) ?f(z),有

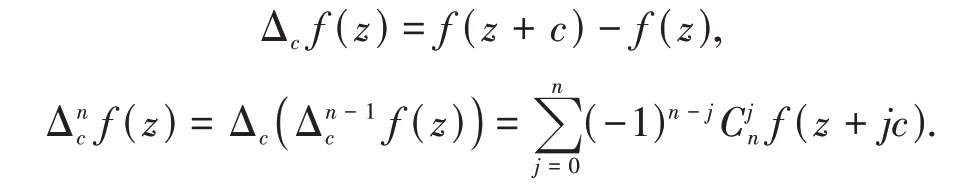
設(shè)a為任意復(fù)數(shù),定義虧量如下:

有窮級(jí)亞純函數(shù)的Nevanlinna 差分模擬理論是由Halburd 等[3]、Chiang 等[4]分別建立的.隨后,Halburd 等[5]等將有窮級(jí)亞純函數(shù)推廣為超級(jí)嚴(yán)格小于1 的亞純函數(shù),這給復(fù)差分方程和唯一性理論的研究提供了強(qiáng)有力的支撐.近年來(lái),不少學(xué)者研究?jī)蓚€(gè)亞純函數(shù)分擔(dān)“2CM+1IM”的問題.

2012年,Chen等研究?jī)蓚€(gè)周期性亞純函數(shù)分擔(dān)“2CM+1IM”,得到如下定理.

定理A[6]設(shè)f(z)和g(z)是以c為周期的非常數(shù)亞純函數(shù)且滿足1 ＜μ(f) ≤ρ(f) ＜∞.假設(shè)ai(i=1,2,3)為可判別的以c為周期的周期函數(shù)且均為f(z)的小函數(shù).若f(z)和g(z) CM 分擔(dān)a1,a2,IM 分擔(dān)a3,同時(shí)滿足

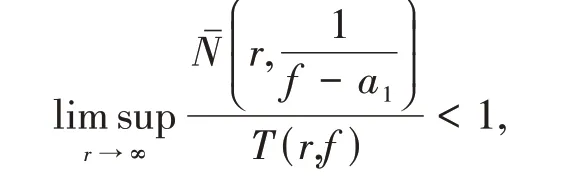
則f(z) ≡g(z).

2020年,Chen等進(jìn)一步研究f(z)及其n階差分分擔(dān)值問題,得到如下定理.

定理B[7]設(shè)f(z)是超級(jí)嚴(yán)格小于1 的超越整函數(shù)且f(z) ?f(z+c).若f(z)和f(z)CM 分擔(dān)0 且IM分擔(dān)1,則f(z) ≡f(z).

同年,Qi等研究f(z)及其n階差分分擔(dān)值問題,得到如下定理.

定理C[8]設(shè)f(z)是超級(jí)嚴(yán)格小于1的超越整函數(shù)且a(≠0)為有窮復(fù)數(shù).若f(z)和f(z)CM分擔(dān)0且IM分擔(dān)a,則f(z) ≡f(z).

在定理B 和定理C 的基礎(chǔ)上增加了f(z)是有理函數(shù)的情況,將f(z)是超越整函數(shù)推廣到f(z)是非常數(shù)亞純函數(shù),得到如下定理:

定理1設(shè)f(z)為超級(jí)小于1 的非常數(shù)亞純函數(shù),c(≠0) ∈C且a(≠0)為有窮復(fù)常數(shù).若f(z)和f(z)CM分擔(dān)0,∞,IM分擔(dān)a,同時(shí)滿足Θ(0,f(z)) ＞0,則f(z) ≡f(z).

注1一些想法來(lái)自文獻(xiàn)[6]和[9].

2 引理

引理1[10-11]設(shè)f(z)為非常數(shù)亞純函數(shù),其超級(jí)ρ2(f)嚴(yán)格小于1,c(≠0)∈C,為任意常數(shù).則

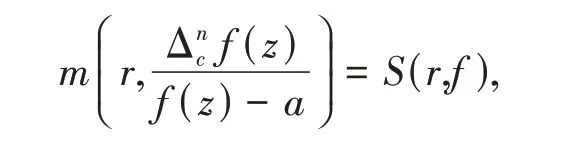
其中r→∞除去一個(gè)對(duì)數(shù)測(cè)度有窮的集合.

引理2[2]設(shè)f(z)是亞純函數(shù),若

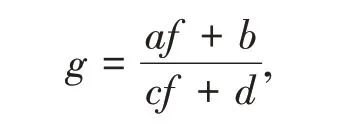
其中a,b,c,d均為f(z)的小函數(shù)并且ad-bc≠0,則T(r,g)=T(r,f) +S(r,f).

3 定理1的證明

情形1f(z)為非常數(shù)有理函數(shù),可設(shè)

結(jié)合分擔(dān)值條件可知存在ε∈(0,1),使得

將式(26)代入式(24)有

這與f(z)是超越的矛盾.

定理1證明完畢.