戴程嘉 劉金強(qiáng) 李春霞

山東省濱州學(xué)院理學(xué)院 (256600)

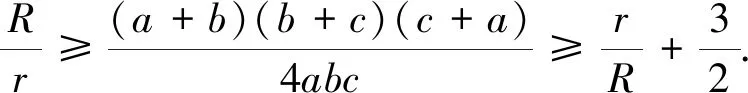
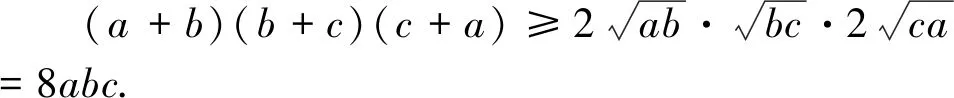
為了給出加強(qiáng)歐拉不等式的幾何意義,本文從下面的命題談起.

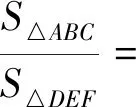
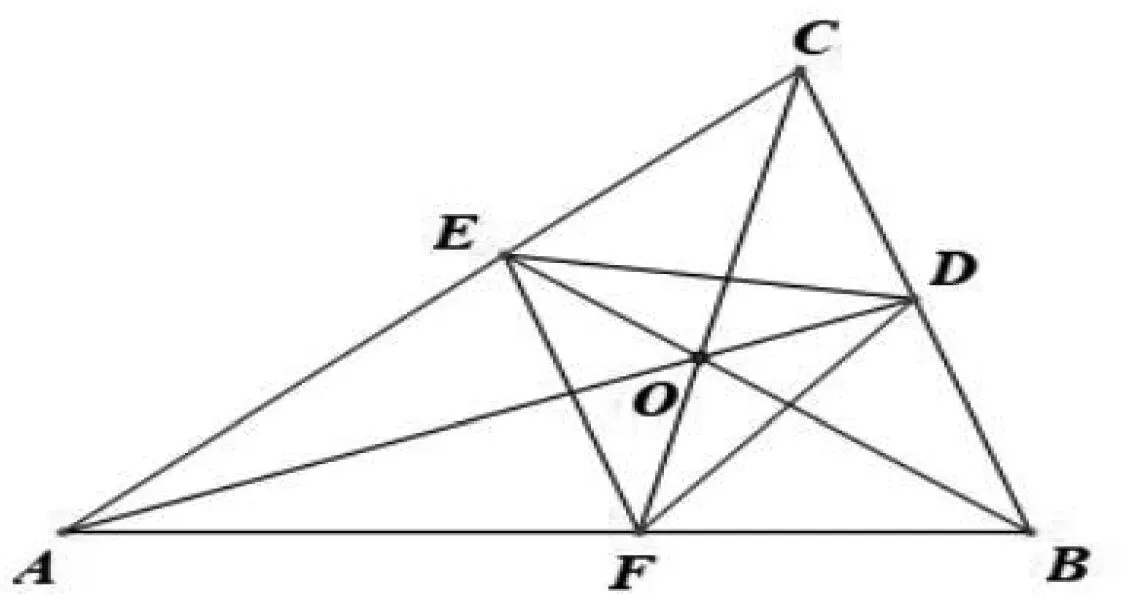
圖1

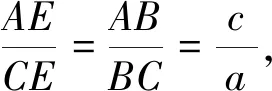
由本文得到的不等式鏈可以推出下面的不等式.

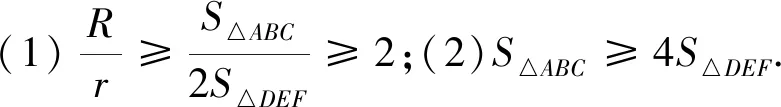
其中(2)是(1)的一部分,(1)是原不等式鏈的幾何表示形式,即任意一個(gè)三角形外接圓半徑和內(nèi)切圓半徑的比值不小于該三角形的面積和三條內(nèi)角平分線與三角形三邊相交形成的新三角形面積的二倍的比值.實(shí)際上利用(1)還能得到一些新的不等式.

命題2 如圖2,在銳角△ABC中,AD,BE,CF為三條內(nèi)角平分線,點(diǎn)M和點(diǎn)N分別為三角形的外心和內(nèi)心,R和r分別為三角形外接圓和內(nèi)切圓的半徑,∠AMC=m,∠BMC=n,∠DNE=p,∠DNF=q,則

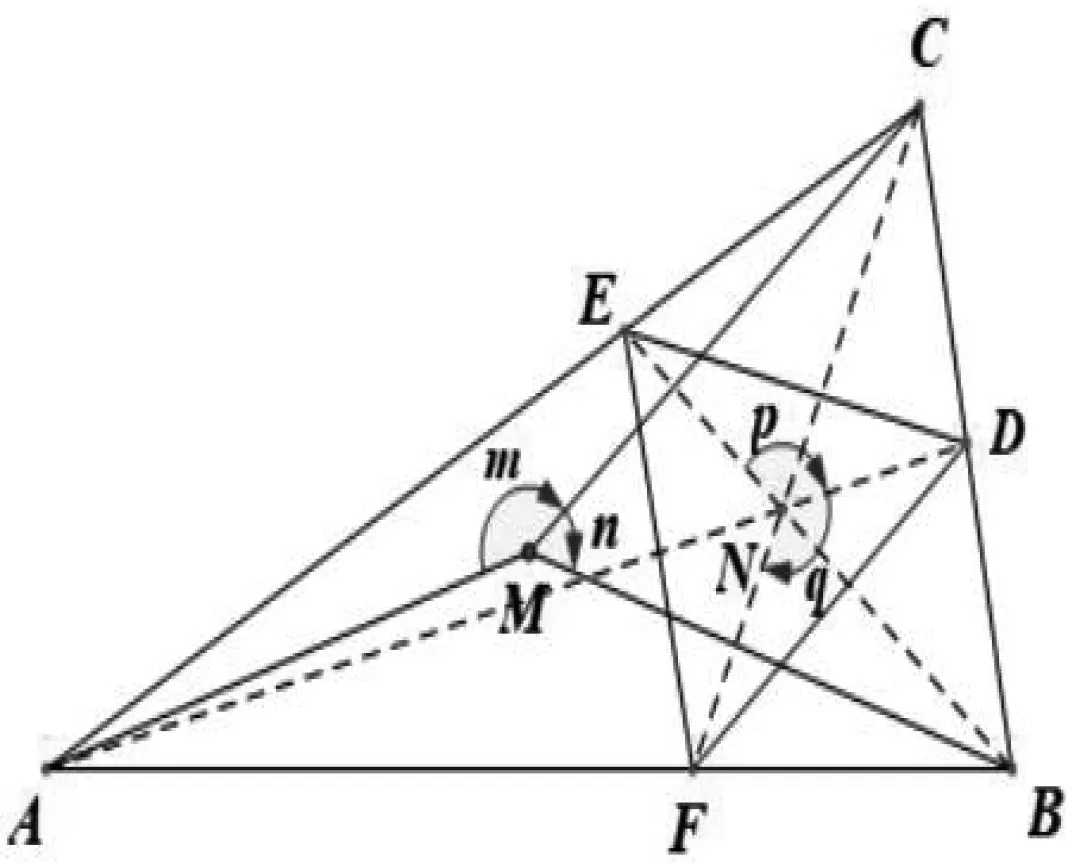
圖2

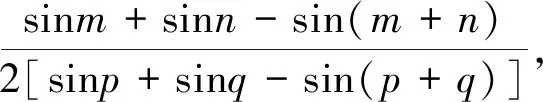
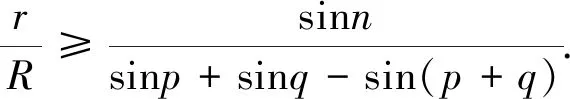
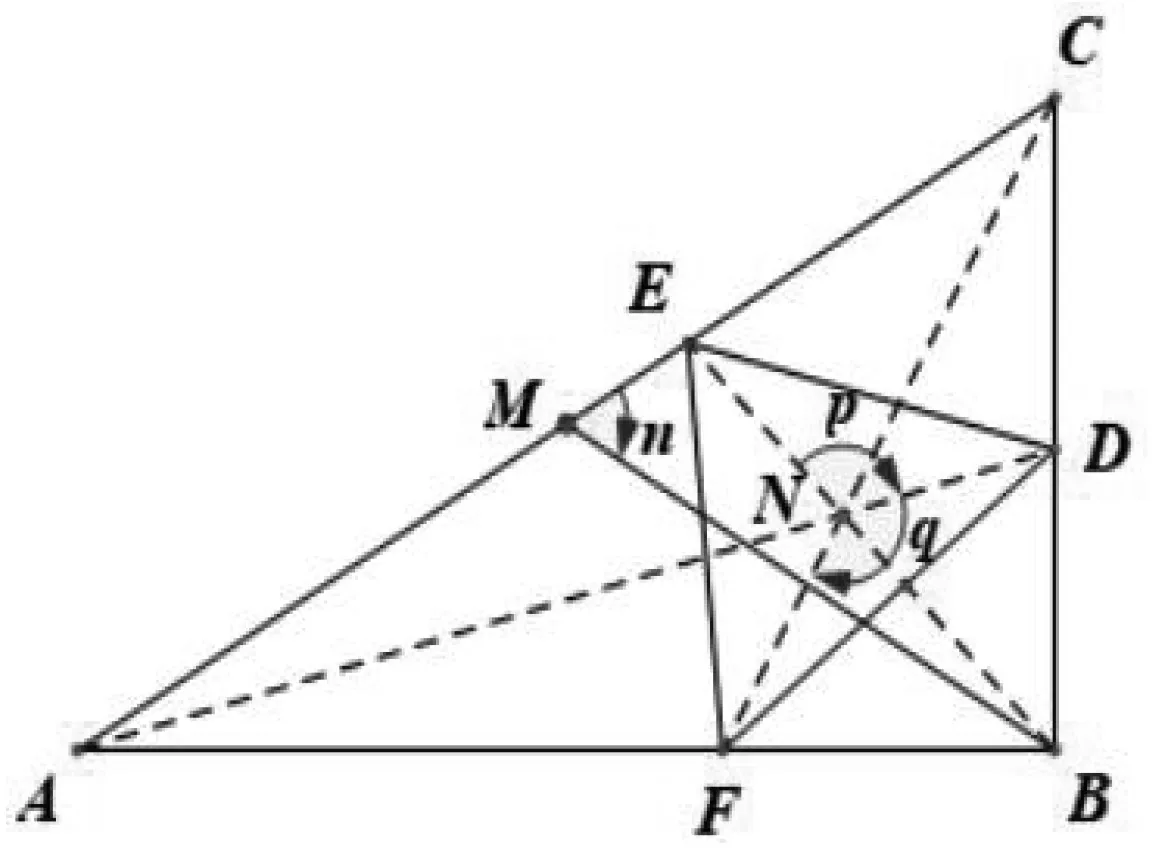
圖3

命題4 如圖4,在鈍角△ABC中,AD,BE,CF為三條內(nèi)角平分線,點(diǎn)M和點(diǎn)N分別為三角形的外心和內(nèi)心,R和r分別為三角形外接圓和內(nèi)切圓的半徑,∠AMC=m,∠BMC=n,∠DNE=p,∠DNF=q,則

圖4

運(yùn)用命題2的方法很容易得到當(dāng)三角形為直角三角形或鈍角三角形的情況,不同的是直角三角形的外心在斜邊上,因此S△ABC=S△ABM+S△CBM,鈍角三角形的外心在三角形外,因此,S△ABC=S△AMC+S△BMC-S△ABM,其余的證明均與命題2的相同,這里就不再贅述了.