汪 文 徐章韜

華中師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)學(xué)院 (430079) 廣東省珠海市廣東實(shí)驗(yàn)中學(xué)金灣學(xué)校 (519040)

筆者在查閱近年的解析幾何高考解答題中,發(fā)現(xiàn)對(duì)于圓錐曲線中定值定點(diǎn)問(wèn)題的考察頻頻出現(xiàn),只不過(guò)考察的形式往往不同,為此,筆者另辟蹊徑,借助曲線系方程求解相關(guān)問(wèn)題,發(fā)現(xiàn)很多問(wèn)題都能迎難而解．

1.相關(guān)概念界定

曲線系方程就是將具有某種共同性質(zhì)的的所有曲線構(gòu)成的集合,采用含有參數(shù)的方程來(lái)表示,這種共同性質(zhì)一般是過(guò)幾個(gè)定點(diǎn)或者交點(diǎn)．對(duì)于一般的二次曲線方程Ax2+2Bxy+Cy2+2Dx+2Ey+F=0,其中有5個(gè)獨(dú)立參數(shù),故一般地5個(gè)獨(dú)立條件能確定二次曲線,從而任意三點(diǎn)不共線的五點(diǎn)確定一條二次曲線．對(duì)于給定的五點(diǎn),若其中三點(diǎn)在直線上,另外兩點(diǎn)不在直線上,則通過(guò)這五點(diǎn)的二次曲線是唯一的,并且是退縮的二次曲線．我們知道過(guò)曲線C1:F1(x,y)=0與曲線C2:F2(x,y)=0交點(diǎn)的曲線系方程為λF1(x,y)+μF2(x,y)=0,同時(shí)若Li:Aix+Biy+Ci=0(i=1,2)表示兩條直線方程,則方程(A1x+B1y+C1)(A2x+B2y+C2)=0可以表示為退化的二次曲線方程．

(1)三條直線的合成(兩條曲線合成的特例)

如圖1,設(shè)Li:Aix+Biy+Ci=0(i=1,2,3)兩兩相交于A,B,C三點(diǎn)(這三點(diǎn)不共線),則曲線系(A1x+B1y+C1)(A2x+B2y+C2)+λ(A2x+B2y+C2)(A3x+B3y+C3)+μ(A3x+B3y+C3)(A1x+B1y+C1)=0包含所有過(guò)A,B,C三點(diǎn)的二次曲線．

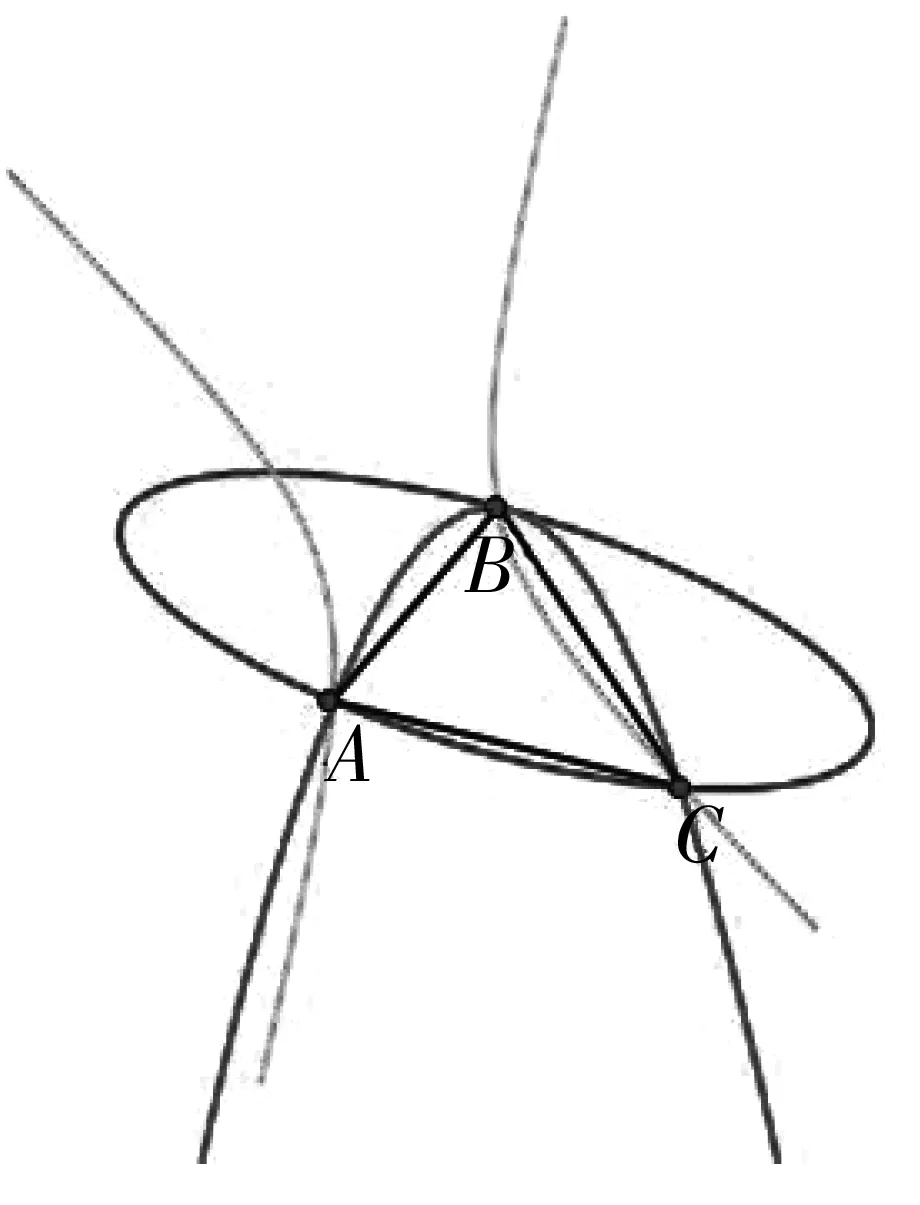
圖1

(2)兩條曲線的合成

兩個(gè)二次曲線C1:F1(x,y)=0,C2:F2(x,y)=0交于不共線的四點(diǎn),則同曲線系λ1F1(x,y)+λ2F2(x,y)=0包含所有過(guò)四交點(diǎn)的二次曲線系方程．若二次曲線有一個(gè)內(nèi)接四邊形,則四條邊所在的直線可分三組:兩組對(duì)邊、一組對(duì)角線,可用兩組對(duì)邊,或一組對(duì)邊和一組對(duì)角線均可合成過(guò)四個(gè)交點(diǎn)的二次曲線系．因此如圖2,圖3,設(shè)Li:Aix+Biy+Ci=0(i=1,2,3,4)為四邊形四條邊所在直線方程或者相對(duì)兩邊與兩條對(duì)角線所在直線方程,則曲線系:(A1x+B1y+C1)(A3x+B3y+C3)+λ(A2x+B2y+C2)(A4x+B4y+C4)=0包含所有經(jīng)過(guò)這四點(diǎn)的二次曲線,其中直線L1,L3為相對(duì)的兩邊或者兩條對(duì)角線所在直線方程.

若過(guò)二次曲線上一定點(diǎn)P作兩條直線L1:A1x+B1y+C1=0,L2:A2x+B2y+C2=0,交二次曲線與另外兩點(diǎn)A,B,如圖4所示,設(shè)直線AB的方程為A3x+B3y+C3=0,由于點(diǎn)P可以看作圓錐曲線上兩個(gè)點(diǎn)無(wú)限靠近匯聚成的點(diǎn),設(shè)圓錐曲線在點(diǎn)P處的切線方程為A4x+B4y+C4=0,則曲線系(A1x+B1y+C1)(A2x+B2y+C2)+λ(A3x+B3y+C3)(A4x+B4y+C4)=0表示過(guò)A,B,P三點(diǎn)的二次曲線．

若把L1·L2=(A1x+B1y+C1)(A2x+B2y+C2)=0理解為退縮的二次曲線系,如果它們與F(x,y)=0有交點(diǎn),那么曲線系F(x,y)+λ(A1x+B1y+C1)(A2x+B2y+C2)=0經(jīng)過(guò)這些交點(diǎn),如果它們有四個(gè)不共線交點(diǎn),那么曲線系包含所有過(guò)此四點(diǎn)的二次曲線．

2.實(shí)例探究

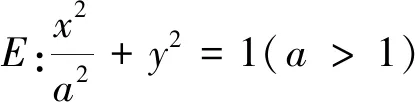
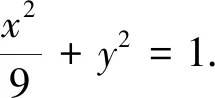
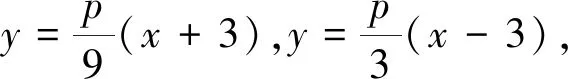
評(píng)注：此題的參考解答比較繁瑣,計(jì)算量偏大,上述借助曲線系方程,簡(jiǎn)化了計(jì)算量,節(jié)約的結(jié)題時(shí)間,效果事半功倍,有興趣的讀者可以查看2020北京卷,2011年四川卷,2010年江蘇卷,解法同上.

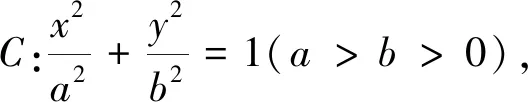
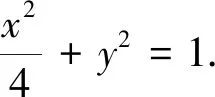
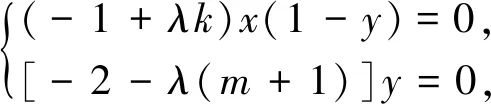
評(píng)注：在處理過(guò)圓錐曲線上一定點(diǎn)作兩條斜率和或者積為定值的直線與圓錐曲線交于另外兩點(diǎn),則這兩點(diǎn)所在的直線過(guò)定點(diǎn)這一類(lèi)問(wèn)題,借助曲線系方程能很快求得所過(guò)定點(diǎn),同時(shí)助曲線系方程也可以求得兩直線的斜率和或者積為定值,比如2013年江西卷和2015年陜西卷2020年山東卷都是這類(lèi)問(wèn)題,有興趣的讀者可以嘗試下.

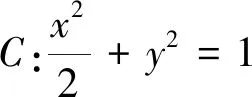
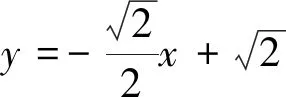
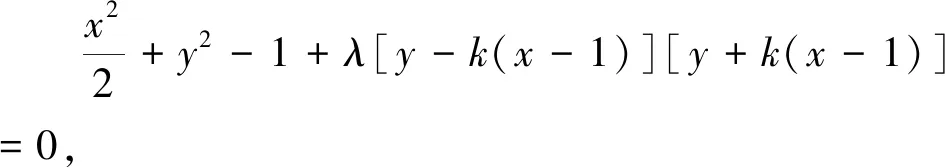
評(píng)注：這類(lèi)高考題屬于過(guò)坐標(biāo)軸上一定點(diǎn)作直線與圓錐曲線交于兩點(diǎn),則再坐標(biāo)軸上存在一定點(diǎn)使得坐標(biāo)軸為所構(gòu)成角的角平分線問(wèn)題,借助曲線系方程可以輕松解決相關(guān)問(wèn)題,比如2015年全國(guó)Ⅰ卷,2018年全國(guó)Ⅰ卷文科就可以采用上述方法來(lái)處理.

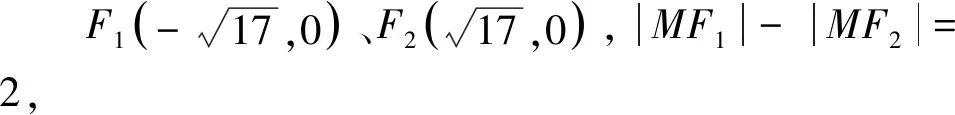
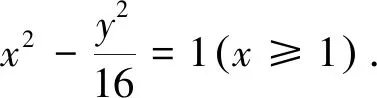
評(píng)注：此題可以直接利用弦長(zhǎng)公式求弦長(zhǎng)進(jìn)行運(yùn)算,或者借助直線的參數(shù)方程來(lái)求解,但采用曲線系方程無(wú)疑是比較簡(jiǎn)潔的求法,對(duì)于圓錐曲線中四點(diǎn)共圓的問(wèn)題,在2011年全國(guó)卷,2104年全國(guó)大綱卷,2016年四川文科卷中也考查到了,有興趣的讀者也可以采用上述方法試試.

縱觀近年的高考題,它們都有很多相似的地方,作為教師的我們,如何找出其相似之處,并能歸納總結(jié)出一般的規(guī)律是值得我們思考的．隨著現(xiàn)代科技的發(fā)展,很多數(shù)學(xué)軟件走進(jìn)數(shù)學(xué)課堂,我們要借助這些軟件探究一些動(dòng)態(tài)過(guò)程中隱藏的規(guī)律,這對(duì)于提高教師自身的教研水平就顯得尤為重要．