靳 龍,陳鴻章

(閩南師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,福建 漳州 363000)

圖G的鄰接矩陣和度對(duì)角矩陣分別記為A(G)和D(G).A(G)的最大特征值(記作ρ(G))稱為G的譜半徑.G的無符號(hào)拉普拉斯矩陣定義為Q(G)=D(G)+A(G),其最大特征值(記作q(G))稱為G的無符號(hào)拉普拉斯譜半徑.Nikiforov[2]定義G的Aα-矩陣(α∈[0,1])為

Aα(G)=αD(G)+(1-α)A(G).

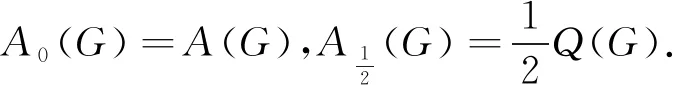
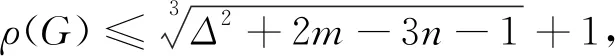
本文將[11]中的結(jié)果推廣到G的Aα-譜半徑ρα(G)上,得到了當(dāng)G不含C3和C4作為子圖時(shí)ρα(G)的可達(dá)上界,同時(shí)也給出了ρα(G)的新的下界.

1 相關(guān)引理

引理1.1[12]設(shè)P(x)是實(shí)系數(shù)多項(xiàng)式,P(Aα(G))的對(duì)應(yīng)于頂點(diǎn)v的行和為Sv(P(Aα(G))),則

min{Sv(P(Aα(G)))}≤P(ρα(G))≤max{Sv(P(Aα(G)))},

其中等式成立當(dāng)且僅當(dāng)P(Aα(G))的各行和都相等.

引理1.2

其中等式成立當(dāng)且僅當(dāng)G為正則圖.

引理1.3[14]設(shè)a1,…,an是正整數(shù),則

2 G的Aα-譜半徑的上界

Filipovski等[11]給出了不含C3和C4作為子圖的圖的譜半徑的上界,我們將其結(jié)果推廣到圖的Aα-譜半徑上.

引理2.1若G不含C3和C4作為子圖,則對(duì)任意α∈[0,1]有

(2-α)αΔ3+(1-α)2Δ2+2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ.

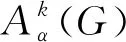
α2D2(G)+α(1-α)D(G)A(G)+(1-α)αA(G)D(G)+(1-α)2A2(G),

故

由于

(αD(G)+(1-α)A(G))(αD(G)+(1-α)A(G))(αD(G)+(1-α)A(G))=

α3D3(G)+α2(1-α)D2(G)A(G)+α2(1-α)D(G)A(G)D(G)+

α(1-α)2D(G)A(G)A(G)+(1-α)α2A(G)D(G)D(G)+(1-α)2αA(G)D(G)A(G)+

(1-α)2αA2(G)D(G)+(1-α)3A3(G).

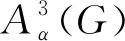
因此

(2-α)αΔ3+(1-α)2Δ2+2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ,

即

(2-α)αΔ3+(1-α)2Δ2+2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ.

根據(jù)引理2.1,有

(2-α)αΔ3+(1-α)2Δ2+2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ.

注2.2若G是k-正則圖,即ρα=δ=Δ=k且m=nk/2,則

注意到A0(G)=A(G),有以下推論.

推論2.3[11]若G不含C3和C4作為子圖,則

推論2.4 若G不含C3和C4作為子圖,則

q3(G)-δq2(G)+δq(G)≤6Δ3+2Δ2(1-δ)+4m-2nδ.

定理2.5 若G不含C3和C4作為子圖,則對(duì)任意α∈[0,1]有

其中

E=(2-α)αΔ3+(1-α)2Δ2+2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ.

證明給定α∈[0,1],設(shè)多項(xiàng)式

p(x)=x3-δ(1-α)x2+(1-α)2δx-E.

注意到

27E2>(1-α)6δ4+18(1-α)3δ2E,

可知p(x)的判別式為

D(p)=-4(1-α)6δ3+(1-α)6δ4+18(1-α)3δ2E-4(1-α)3δ3E-27E2<0.

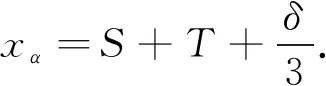
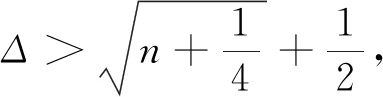
證明用Newton-Raphson方法[16]逼近如下多項(xiàng)式的實(shí)根:

p(x)=x3-δ(1-α)x2+(1-α)2δx-((2-α)αΔ3+(1-α)2Δ2+

2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ).

由于

p(δ)=αδ3+(1-α)2δ2-((2-α)αΔ3+(1-α)2Δ2+

2(1-α)2m-(1-α)2nδ-α(1-α)Δ2δ)<0,

p(Δ)=(1-2α+α2)Δ3-(1-α)2(δ+1)Δ2+(1-α)2δΔ-2(1-α)2m+(1-α)2nδ>0,

故p(x)有唯一的實(shí)根xα∈(δ,Δ).取初始值x0=Δ進(jìn)行迭代,計(jì)算第一次迭代可得

由于函數(shù)p(x)在區(qū)間[xα,Δ]上是下凸的,故p(x)在點(diǎn)(Δ,p(Δ))處的切線與x軸的交點(diǎn)在xα的右側(cè).所以ρα(G)≤xα≤x1.

3 G的Aα-譜半徑的下界

Nikiforov[2]給出了G的Aα-譜半徑的下界:

(1)

其中等式成立當(dāng)且僅當(dāng)G為正則圖.本節(jié)利用G的頂點(diǎn)度的方差

對(duì)上述結(jié)果進(jìn)行改進(jìn).設(shè)G的度序列為Δ=dv1≥dv2≥…≥dvn=δ.

定理3.1對(duì)任意α∈[0,1]都有

(2)

其中等式成立當(dāng)且僅當(dāng)G是正則圖.

證明由引理1.2和引理1.3可得

(3)

注意到

并且

代入(3)便得到

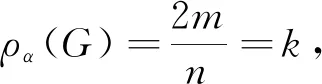
注3.2文獻(xiàn)[17]給出了G的Aα-譜半徑的如下下界:

(4)

定理3.3

(5)

其中等式成立當(dāng)且僅當(dāng)G為正則圖.

證明我們有

(6)

由引理1.2可得

(7)

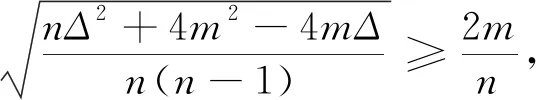
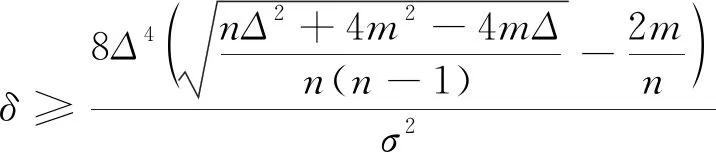
結(jié)合定理3.1和3.3,可得

定理3.6

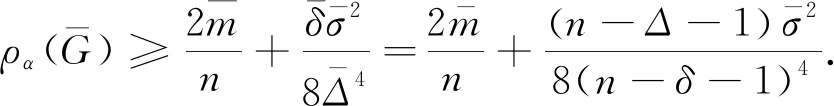
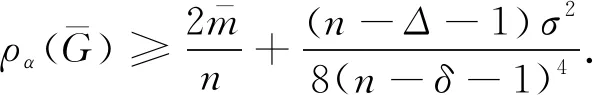
定理3.7

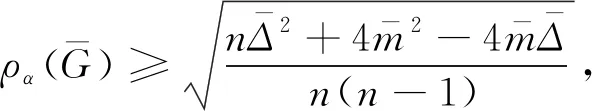
致謝本文得到數(shù)字福建氣象大數(shù)據(jù)研究所和數(shù)據(jù)科學(xué)與統(tǒng)計(jì)重點(diǎn)實(shí)驗(yàn)室的資助.