◇ 江蘇 楊歡濤

函數(shù)對稱性的類比推理與數(shù)理證明

◇ 江蘇 楊歡濤

函數(shù)的基本性質(zhì)在高中課程標準中是難點也是重點,同時在高考要求上屬于C級,所以我們在高考題或調(diào)研考試的中檔題中經(jīng)常見到如“函數(shù)f(x)關(guān)于x＝a對稱”或“f(a＋x0)＝f(a－x0)”的題設條件.研究高中數(shù)學中函數(shù)的性質(zhì)往往繞不開函數(shù)的對稱性,而事實上高中數(shù)學中許多函數(shù)不僅具有優(yōu)美的對稱圖象,而且還具有優(yōu)美的對稱表達式.眾所周知,對稱關(guān)系存在軸對稱和中心對稱之分,本文嘗試從數(shù)學推理和理論證明的角度來討論函數(shù)對稱性.

1 軸對稱函數(shù)對稱性類比與論證

學生最熟悉的軸對稱函數(shù)非偶函數(shù)莫屬.偶函數(shù)關(guān)于y軸對稱,因此有f(x)＝f(－x).關(guān)于y軸對稱,其實質(zhì)是關(guān)于x＝0對稱.

1)類比推理.

如圖1,函數(shù)y＝f(x)關(guān)于直線x＝a(a＞0)對稱,以“偶函數(shù)關(guān)于x＝0對稱,則f(x)＝f(－x)”為基礎,不難推理得出結(jié)論:“若函數(shù)y＝f(x)關(guān)于直線x＝a對稱,則f(a＋x)＝f(a－x).”其類比推理過程如下:關(guān)于直線x＝a對稱的函數(shù)f(x),可看成由關(guān)于x＝0對稱的函數(shù)平移得來,原圖象上一組對稱點P和P′,平移后在新圖象上對應的坐標可分別記為(a＋x,f(a＋x))和(a－x,f(a－x)).因為這是一組對稱點的水平移動,縱坐標大小不變,顯然存在f(a＋x)＝f(a－x).反之,上述命題的逆命題也成立,即:“若f(a＋x)＝f(a－x),則若函數(shù)y＝f(x)關(guān)于直線x＝a對稱.”當然這僅僅是邏輯上推演,要證明命題“若函數(shù)y＝f(x)關(guān)于直線x＝a對稱,則f(a＋x)＝f(a－x)”,必須有充分的理論證明.

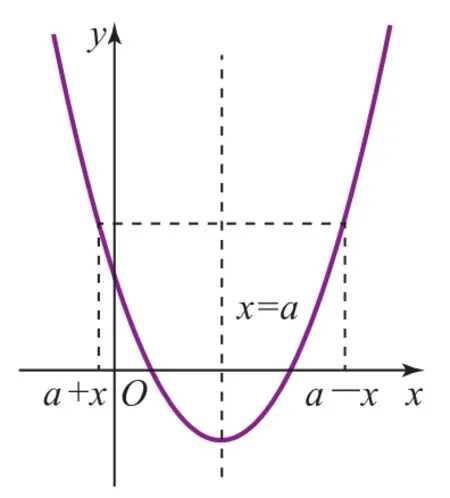
圖1

2)理論證明.

證明命題“若函數(shù)y＝f(x)關(guān)于直線x＝a對稱,則f(a＋x)＝f(a－x)”,需要從充分性和必要性2方面進行說明.充分性證明:不妨設函數(shù)上任意點P坐標為(a＋x,f(a＋x)),由軸對稱的性質(zhì)易知點P關(guān)于直線x＝a對稱點P′也在函數(shù)f(x)的圖象上,其坐標滿足函數(shù)y＝f(x)的表達式.根據(jù)中點坐標公式易得xP′＝a－x,所以點P′的縱坐標yP′＝f(ax).又因為點P與點P′關(guān)于直線x＝a對稱,所以f(a＋x)＝f(a－x).必要性證明:在函數(shù)y＝f(x)的圖象上任取一點P記其坐標為(a＋x,f(a＋x)),若點P關(guān)于x＝a的對稱點也在函數(shù)圖象上,則函數(shù)y＝f(x)關(guān)于直線x＝a對稱.易知P關(guān)于直線x＝a對稱點的橫坐標為xP′＝a－x,根據(jù)對稱關(guān)系顯然P′的縱坐標可記為yP′＝f(a＋x).又因f(a＋x)＝f(a－x),所以點P′的坐標可記為(a－x,f(ax)),所以P′的坐標滿足函數(shù)y＝f(x)的關(guān)系式,即點P′也在函數(shù)圖象上,所以必要性得證.

3)補充證明.

結(jié)論1:若函數(shù)y＝f(x)關(guān)于直線x＝a對稱,則f(x)＝f(2a－x).不妨令上述結(jié)論中的a＋x＝t,移項后可得x＝t－a,以t－a替換x,顯然a－x＝2at,因此就存在f(t)＝f(2a－t),也即f(x)＝f(2ax).不妨設結(jié)論1中的2a＝b,則結(jié)論1的形式就可變?yōu)榻Y(jié)論2:若函數(shù)y＝f(x)關(guān)于直線x＝對稱,則f(x)＝f(b－x).借助上述理論證明過程,不難證明結(jié)論3:若函數(shù)y＝f(x)關(guān)于直線對稱,則f(a＋x)＝f(b－x).

2 點對稱函數(shù)對稱性的分析與證明

關(guān)于點(中心)對稱函數(shù)的對稱表達式又呈現(xiàn)出什么樣的形式呢?這可從奇函數(shù)對稱性表達式的類比中窺得一斑,并且通過理論的證明來印證.

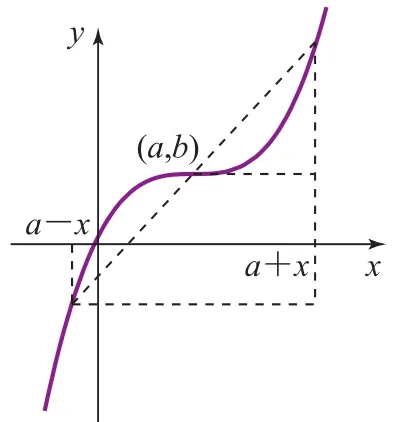
圖2

1)類比推理.

眾所周知,奇函數(shù)關(guān)于原點對稱,其對稱表達式為f(x)＋f(－x)＝0,以此為基礎,不難類比出命題:若函數(shù)y＝f(x)關(guān)于點(a,b)對稱,則f(a＋x)＋f(a－x)＝2b.如圖2不妨假設a＞0、b＞0,則函數(shù)y＝f(x)可視為原奇函數(shù)向右平移a個單位,再向上平移b個單位形成,在此過程中原圖象上任意一組對稱點P和P′,在平移后其對應坐標分別可記為(a＋x,f(a＋x))和(a－x,f(a－x)),根據(jù)中心對稱的特性(對稱點連線經(jīng)過對稱點且被對稱點平分)并結(jié)合中點坐標公式可得f(a＋x)＋f(a－x)＝2b.同樣,其逆命題也成立,即:“若f(a＋x)＋f(a－x)＝2b,則y＝f(x)關(guān)于點(a,b)對稱.”

2)理論證明.

充分性證明:在y＝f(x)上任取一點P(a＋x,f(a＋x)),根據(jù)中心對稱的性質(zhì),易知點P關(guān)于點(a,b)中心對稱點P′也在f(x)的圖象上,其坐標應滿足函數(shù)y＝f(x)的表達式.根據(jù)中點橫坐標公式易得xP′＝a－x,所以點P′的縱坐標yP′＝f(a－x),利用中點縱坐標公式可得f(a＋x)＋f(a－x)＝2b.

必要性證明:在函數(shù)y＝f(x)的圖象上任取一點P記其坐標為(a＋x,f(a＋x)),若點P關(guān)于點(a,b)中心對稱點P′也在函數(shù)f(x)的圖象上則函數(shù)y＝f(x)關(guān)于點(a,b)對稱.易知點P關(guān)于點(a,b)中心對稱點的橫坐標為xP′＝a－x,根據(jù)對稱關(guān)系顯然P′的縱坐標可記為yP′＝2b－f(a＋x).又因為f(a＋x)＋f(a－x)＝2b,所以點P′的坐標可記為(a－x,f(a－x)),所以P′的坐標滿足函數(shù)y＝f(x)的關(guān)系式,即點P′也在函數(shù)圖象上,所以必要性得證.

3)補充說明.

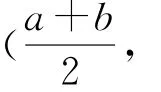
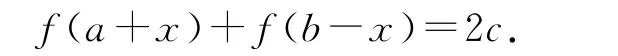
反思上述函數(shù)對稱性的邏輯推理與數(shù)理證明過程,不難發(fā)現(xiàn)這種對稱性的結(jié)論與奇偶函數(shù)對稱性結(jié)論存在極大的相關(guān)性.因為偶函數(shù)關(guān)于y軸對稱,奇函數(shù)關(guān)于原點對稱,所以只需要研究其在區(qū)間(－∞,0)上的性質(zhì),就可知道函數(shù)在對應區(qū)間(0,＋∞)的圖象和性質(zhì).而上述對稱性結(jié)論是研究函數(shù)在區(qū)間(－∞,a)上的圖象和性質(zhì),就可知道函數(shù)在其對稱區(qū)間(a,＋∞)上的圖象和性質(zhì).所以上述對稱思想研究函數(shù)的圖象和性質(zhì)可以看成奇、偶函數(shù)對稱性結(jié)論的推廣.

(作者單位:江蘇省蘇州市第一中學)