Vision tracking based on improved similarity measurement of spatiogram and particle filter
YIN Mingfeng, ZHU Jianliang, BO Yuming, ZHAO Gaopeng, WU Panlong
(School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China)
Abstract: Spatiogram is a generalization of the histogram, which can more accurately describe the image as it can capture higher-order spatial moments. In view that selecting a suitable similarity measurement is critical for spatiogram based object tracking, an effective spatial histogram similarity measurement is proposed based on the correlation degree between the target/local background (CTLB) and Jensen-Shannon divergence (JSD). The CTLB coefficient is calculated to weight each bin’s contribution of spatiogram in complex scene, which can reduce the disturbance of background information. The spatial similarity is computed with JSD, regarding the spatial distribution of pixels corresponding to each bin as a Gaussian distribution. Finally, the proposed measurement method is compared with existing methods in the framework of Particle Filter. The mean tracking errors in the two testing sequences are 3.47 pixels and 4.36 pixels respectively, which indicate that the proposed method gives superior discriminative ability and performs more accurately and robustly in the tracking process.
Key words: spatiogram; similarity measure; particle filter; vision tracking
As an important branch of computer science, visual tracking[1-5]is widely applied in many fields, such as Video Surveillance, Human-Computer Interaction, Virtual Reality and any more. How to implement a robust and efficient tracking process becomes a research focus in video sequences. Recently, a large number of vision tracking algorithms have been proposed, which can be divided into two classes: deterministic and stochastic modeling method. Mean-shift (MS)[6-7]and Particle Filter(PF)[8]are the typical algorithms of these two classes algorithms. Mean-shift has a high speed in visual tracking while the algorithm converges to the local minimum easily and is difficult to capture fast-moving target. Particle filters are simple, robust, and effective, and have obtained success in many challenging tasks. Particle filters simultaneously track multiple hypotheses and recursively approximate the posterior probability density function (pdf)in the state space with a set of randomly sampled particles.Both the appearance model and the similarity measure are very important to the performance of particle filters as a reason of the particles are weighted according to a similarity measure and the sampling of particles is also dependent on the similarity measure.
In visual tracking, object representation is an important issue, because it can describe the correlation between the appearance and the state of the object. An appropriate object representation makes the target model more distinguishable from the background and achieves a better result. Color histogram[9]is a widely used method in object representation as a reason of simple calculation and high real time. It counts the frequency of certain feature patterns but ignores the spatial information,hence it’s suitable for modeling non-rigid objects and robust against many spatial transformations. However, it may perform poorly if the background presents confusing colors as a result of lacking spatial structure information.To overcome this limitation, Wang[10]proposed SMOG(Spatial-color Mixture of Gaussians), in which the statistical characteristics of both color and spatial are calculated. Birchfield[11]proposed the concept of the spatial histogram, or spatiogram[12-14], in which each histogram bin contains the mean and covariance information of the locations of pixels belonging to that bin.Spatiogram presents promising performance in image retrieval and vision tracking and has attracted increasing research attentions in recent years. In the process of object representation, the information of background’s pixels are included inevitably when trying to contain the target’s information as much as possible. Thus, the object representation with the involvement of confusing colors from background usually makes inexact target’s appearance model, which leads to bad performance or losing target in the process of tracking. In order to solve the above problem, the correlation degree between the target and local background (CTLB) was proposed in this paper. The CTLB is calculated by the color histogram of the target and local background. Motivated by CTLB, we propose a new similarity measure of the spatial histogram, which has superior discriminative power.
In this paper, we propose an effective similarity measure of spatiogram representation in the context of improving the performance of particle filters. This paper is organized as follows: In section 1, we briefly describe the particle filter theory. In section 2, we present a novel similarity method of spatiogram representation based on the correlation degree between the target and local background, and then the flow of the proposed algorithm is given to illustrate how to apply the new similarity method in particle filter. In section 3, we demonstrate experimentally the advantages of our new measure over existing measures and give our conclusion in section 4.
1 Visual tracking in the framework of particle filter
Particle Filter is a filtering method based on Monte-Carlo and Bayes Estimation methods, which is used to solve the object tracking problem under the conditions of non-Gaussian and nonlinear recently.Consider the following time series target tracking problem

Prediction:

Update:
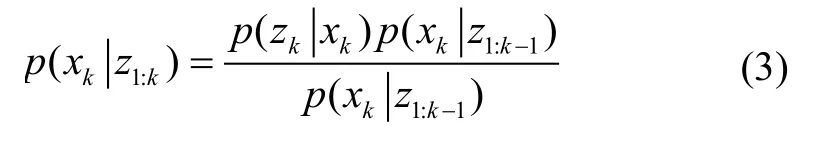
The Bayesian optimal estimation can be obtained from Eq. (2) and (3), while the analytical solution not under many conditions. Thus, approximate methods are applied to solve this problem, and PF is one kind of method to get the result efficiently. PF transforms the integral operation to summation operation of finite set,therefore, the posteriori probabilitycan be described as


We choose the prior distributionas importance sampling function, then Eq.(5) can be simplified as


In a tracking approach the estimated state is updated at each time step by incorporating the new observations. Taking color histogram and Bhattacharyya distance as target representation model and similarity measure for example, we definethe target model andthe model of the candidate zone represented by thejth particle, thus the coefficient between the above two models is defined as


which is called the Bhattacharyya distance. So, the likelihood of thejth particle can be calculated as

2 The proposed algorithm
2.1 Spatiogram representation
Birchfield[11]has proposed the concept of histograms yielding spatiograms. Comparing to histograms,spatiograms capture higher-order spatial moments. A second-order spatiogram model of an object is identical to a histogram of its features, except that it also stores additional spatial information, namely the mean and covariance of the spatial position of all pixels that fall into each histogram bin. We represent the second-order spatiogram withbins of an image as



2.2 Similarity measure of spatiogram
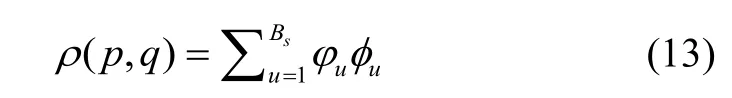

2.3 The correlation degree between target and local background
In the process of visual tracking, the target zone is usually illustrated by rectangle or ellipse window. The background information is involved in target appearance model inevitably when trying to contain all the parts of the target. The involvement of the background information makes the appearance model inexact and decreases the discriminability of similarity measure between representation models, which cannot ensure the performance of tracking algorithm. Thus, it is necessary to consider the influence of background information in the similarity measure.
In this paper, the correlation degree between the target and local background (CTLB) is imported to reduce the disturbance of background information. The CTLB coefficient is adapted to measure the contribution of each bin with the changes of the complex scene. As shown in figure 1(a), we use a “center-surround” approach to sample the pixels from object and background. A rectangle set of pixels covering the object is chosen to represent the object pixels, while a larger surrounding ring of pixels is chosen to represent the background. For an inner rectangle of dimensionsan outer margin of widthand heightpixels forms the background sample. In figure 1(a), the target is represented by red rectangle while its local background is represented by the ring region of the red rectangle in the green rectangle.



Fig.1 (a) The walker is selected in the test scene, and the target and local background region is marked; (b) Two histograms of interest region; (c) The likelihood ratio and the weight coefficient; (d) Weight image
2.4 The proposed similarity measure
In this paper, a new similarity measure using CTLB and Jensen-Shannon divergence (JSD) is proposed to improve the discriminability of spatiogram. JSD is extension measure based on Kullback-Leibler divergence(KL divergence), a well-motivated and widely used distance measure from information theory.
In order to calculate the spatial similarity measure of spatiogram conveniently, here, the pdf of the spatial locationin theuth bin is approximated by a Gaussian distribution,


The definition of the KL divergence[15]is used as a dissimilarity measure between two distributionsand

Note that the KL divergence is not symmetric. In our framework we follow common practice and use the Jenson-Shannon divergence as a smoothed and symmetrized version instead.withTo obtain a closed-form solution, we approximate the mixtureby a Gaussian
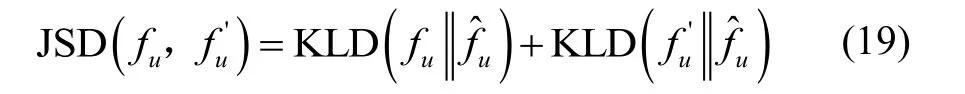

So, the Jensen-Shannon divergence[15]can be obtained by:

Usually the range of similarity score is normalized to [0, 1]. Hence we choose spatial similarity measureto be

In this way, we obtain our JSD and CTLB based spatiogram similarity measure as

where the color feature similarity measureHere, we name the proposed similarity measure as WJSD as a reason of using the weight function
2.5 Algorithm outline
In this paper, a new vision tracking algorithm in the framework of particle filter is designed, in which spatiogram is used to represent target and an improved similarity measure is adopted to increase the discriminability of spatiogram. This proposed algorithm can be summarized as follows:
Step1.Normalization:select the target rectangle region with center pointand generate the initial particlesthen calculate the spatiogram representation model and CTLB according to Eq.(12) and Eq.(16).
Step2.Prediction:the state of particles change by the second-order AR dynamics,

Step3.Measurement: compute the similarity measure between the candidate model and target model represented by spatiogram, and the observation probabilityaccording to Eq.(10) and Eq.(23).
Step4.Estimation: update the weight of particles according to Eq.(6) and calculate the state estimationusing Eq.(7).
Step5.Update the representation model of the target.
Step6.Resampling, resample the particles from
Step7.Turn to step 2 if vision series continues,otherwise step out.
In order to cope with the changes of target appearance during tracking, we adopt template updating to the tracking framework in order to reduce accumulative error and improve the accuracy of the algorithm. In this paper, a template buffer is constructed to save the efficient appearance model and the similarity of each model, which can storeLmodels at most. The appearance model manual selected in the first frame is saved as the initial template in the buffer and used to template match. In the process of matching, fusing the appearance model of the current positionand the current template when the matching coefficient is greater than the threshold, we can get the new template
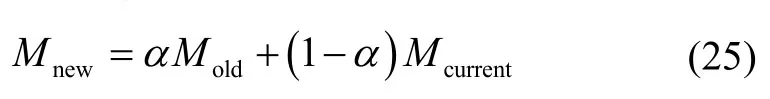
3 Experiments and analysis
3.1 Comparing the discriminative ability
In the experiment, thex-offset andy-offset for the object with rectangle box in Fig.2 are added to measure the similarity. The similarity score should peak when there is no offset and decrease rapidly as the offset increase. As shown in Fig.3, the similarity measure method proposed in this paper gave best overall performance.

Fig.2 The object of interest. The walking man is chosen as the target model

Fig.3 Scores of each similarity over X direction and Y direction.Comparison among three similarity measures: the proposed measure (blue), JSD measure (red), Brichfield’s method (green).
3.2 Vision Tracking Experiments
Four challenging sequences with different variations are exploited to evaluate our tracking system. These sequences are Caviar, Woman, and Headtracker. These sequences cover the four main challenges of object tracking, which are partial and full occlusion, the variation of illumination, pose and scale variation and confused background, respectively. Each of the test datasets has its own focus on these challenges. Caviar datasets focus on complicated occlusion and variation of pose, scale and background, the target of which are walking man. Woman datasets focus on the partial occlusion and scale variation and illumine- tion changes, the target of which is human being with a moving view. Headtracker sequences focus on the confuse background and scale variation, the target of which is head of moving human.

Fig.4 Examples of tracking results for three measures:proposed measure (red), JSD measure (blue), Brichfiled’s measure (black).The frame’s number is marked on the pictures.
Particle filter is applied to track the object, and compared among JSD measure, Brichfield’s measure and the proposed measure. The Euclidean distance of the centers of the tracked object from the ground truth location is computed to evaluate the tracker’s stability and accuracy,


Fig.5 Curves of tracking distance errors of Caviar datasets

Tab.1 Tracking errors of Caviar sequence
The bounding box areas of three trackers in the original images are shown in different rows in Fig.4,where comparison results on Caviar are shown. We select the frames with occlusions and drastic changes.
Our results are marked by red rectangle bounding box.We can see that the proposed tracker performs well in the frames with the occlusion, comparing to the other two trackers. In detail, from frame 68 to frame 121, the moving human encounters occlusion and confuse object. From this process, we can see that the proposed measurement method can handle the occlusion and have an accurate location result, comparing to JSD and Brichfield measures.The proposed measure can distinguish the object from the background accurately as a reason for our method considering the effect of background information.
Fig.6 demonstrates how accurate and robust our method is when the object undergoes occlusion. In the process of tracking, the moving woman encounters five times of partial occlusion. Tab.2 also shows that the proposed method achieves the best accurate and stable tracking performance, similar to Tab.1.
One additional dataset is used to illustrate the advantage of the proposed method when encounters confusing target which is shown in Fig.8 and Fig.9. Twosequences named as “seq_villains1” and “seq_jd” are used to demonstrate the tracking algorithm. Both the objects of interest in the two sequences are head of moving human. In “seq_villains1”, the target undergoes the confuse object from frame 21 to frame 70 and from frame 105 to frame 199. In “seq_jd”, the confuse object appears from frame 16 to frame 20 and from frame 83 to frame 94. Our method can handle this situation correctly and get the accurate location.

Tab.2 Tracking errors of Woman sequence

Fig.6 Examples of tracking results for three measures:proposed measure (red), JSD measure (blue), Brichfield’s measure (black). The frame’s number is marked on the pictures.

Fig.7 Curves of tracking distance error of Woman sequences

Fig.8 Sample frames of tracking result for the proposed method in “seq_villains1”: the blue rectangle is the bounding box of target

Fig.9 Sample frames of tracking result for the proposed method in “seq_jd”: the blue rectangle is the bounding box of target
4 Conclusion
This paper presents a novel similarity measure for spatial histogram based image representation, which is based on JSD divergence and CTLB coefficient. The proposed measure increases the discriminative ability of spatial histogram representation. Our comprehensive experiments prove that the performance of our proposed measure for object tracking tasks and the tracking results are very promising.

