Shifeng Ding,Zile Jiang,Sanjay K.Bose,Gangxiang Shen

1 School of Electronic and Information Engineering,Soochow University,Jiangsu,China

2 Suzhou Key Laboratory of Advanced Optical Communication Network Technology,Soochow University,China

3 Jiangsu Engineering Research Center of Novel Optical Fiber Technology and Communication Network,Soochow University,China

4 Department of Information Engineering,The Chinese University of Hong Kong,Hong Kong,China

5 Kuang Yaming Honors School,Nanjing University,Jiangsu,China

6 Department of EEE,IIT Guwahati,Guwahati,India

Abstract: Network virtualization is important for elastic optical networks(EONs)because of more flexible service provisioning.To ensure guaranteed quality of service (QoS) for each virtual elastic optical network (VEON),clients usually request network resources from a network operator based on their bandwidth requirements predicted from historical traffic demands.However,this may not be efficient as the actual traffic demands of users always fluctuate.To tackle this,we propose a new VEON service provisioning scheme,called SATP,which consists of three stages,i.e.,spectrum assignment(SA),spectrum trading (ST),and spectrum purchasing (SP).Unlike conventional once-for-all VEON service provisioning approaches,the SATP scheme first allocates spectrum resources to VEONs according to their predicted bandwidth requirements with a satisfaction ratio α (0 ＜α ≤1).Then,to minimize service degradation on VEONs which are short of assigned spectra for their peak traffic periods,the scheme allows VEONs to trade spectra with each other according to their actual bandwidth requirements.Finally,it allows VEON clients to purchase extra spectrum resources from a network operator if the spectrum resources are still insufficient.To optimize this entire process,we formulate the problem as a mixed integer linear programming (MILP) model and also develop efficient heuristic algorithms for each stage to handle large test scenarios.Simulations are conducted under different test conditions for both static and dynamic traffic demand scenarios.Results show that the proposed SATP scheme is efficient and can achieve significant performance improvement under both static and dynamic scenarios.

Keywords:virtual elastic optical network;virtual optical network embedding;spectrum assignment;spectrum trading;spectrum purchasing

I.INTRODUCTION

To meet the stringent requirements of 5G communications on data rates,latency,and reliability,elastic optical network (EON),one of the most promising optical networking solutions,has been enhanced with many new techniques[1].Among these,network virtualization is especially attractive because of its operational agility,quality of service (QoS) guarantee,and lower capital expenditure (CAPEX)[2].Based on the virtualization concept,a traditional Internet service provider (ISP) is functionally divided into an infrastructure provider and a service provider[3].By sharing substrate networks managed by the infrastructure provider,the service provider may own multiple self-contained virtual elastic optical networks(VEONs)tailored for specific services or applications.In general,VEON services are provisioned through a mapping process referred to as virtual optical network embedding (VONE)[4].To guarantee QoS of a VEON,most VONE approaches allocate fixed resources according to clients’maximum bandwidth requirement,predicted based on their historical traffic demands (more specifically,peak traffic demands in most cases).However,such prediction cannot guarantee its accuracy and the actual traffic demand of each VEON usually fluctuates over time and its peak traffic may only occur randomly,for fairly short times.Therefore,this approach may lead to severe underutilization of network resources.To tackle this inefficiency,in the previous works[5,6],the authors proposed a scheme called spectrum trading between VEONs to allow them to trade their resources according to their actual traffic demands.This however only considers spectrum resources that have already been allocated to VEONs.It may not be sufficient to satisfy user demands and it is quite possible that the new user traffic cannot be fully carried even with the use of the idle allocated resources through spectrum trading,and therefore,the quality of service(QoS)of these VEONs may be degraded.

To resolve this problem,we propose a new VEON provisioning scheme called SATP that consists of three stages,i.e.,spectrum assignment(SA),spectrum trading (ST),andspectrum purchasing (SP).Specifically,the SA stage handles spectrum resource allocation to each VEON according to its predicted bandwidth requirement based on a certain satisfaction ratioα(0＜α ≤1).Here,by setting a properα,we aim to reduce the CAPEX of each VEON at the cost of a certain level of service degradation.To tackle the service degradation because of a smallα,we further consider the ST stage to allow different VEONs to trade their spectrum resources with each other,according to their actual bandwidth requirements,using the ST mechanism proposed in[5,6].However,the ST scheme may still not be able to guarantee QoS for each VEON if there are very high traffic surges on them.To handle this,we further propose the SP stage to allow VEONs that need more spectrum resources to purchase them directly from the network operator so that the QoS can be guaranteed for each VEON.

The novelty of this work is that a complete VEON service provisioning scheme is proposed,integrating all the stages of spectrum assignment,spectrum trading,and spectrum purchasing.Another significant contribution of this work is that it addresses,for the first time,the important issues of when and how to purchase minimum additional spectrum resources required from the network operator to meet the QoS requirement of each VEON.The addition of spectrum resource purchasing and the optimal integration of the spectrum trading and purchasing stages is a significant enhancement over the previous works in[5,6].

The detailed contributions of this paper are summarized as follows.We propose an integrated VEON service provisioning scheme called SATP,which consists of spectrum assignment,spectrum trading,and spectrum purchasing.The scheme can improve the spectrum utilization of virtualized EONs and minimize costs paid by VEON clients while guaranteeing their QoS.We formulate the SATP problem as a mixed integer linear programming(MILP)model and develop heuristic algorithms to obtain efficient solutions.We conduct simulations and evaluate the efficiency of the SATP scheme under different test conditions in both static and dynamic bandwidth demand scenarios.Results show that,in a static scenario,the proposed scheme can significantly reduce the cost paid by VEON clients compared to a benchmark scheme that does not apply these strategies.We also find that even in a dynamic scenario,it can significantly reduce VEON blocking probability and the amount of lost traffic in VEONs served by the system.

The remainder of this paper is organized as follows.Section II reviews the related work of this study.In Section III,we introduce the basic concept related to the SATP scheme.In Section IV,we define the SATP problem and formulate it as an MILP model.Efficient heuristic algorithms are introduced in Section V.In Section VI,we conduct simulations under different test conditions to verify the efficiency of the proposed scheme.Finally,Section VII concludes this paper.

II.RELATED WORK

Previous studies on VONE for service provisioning in a virtualized optical network have considered applying a basic embedding strategy to achieve a specific objective such as minimizing embedding cost,maximizing virtual optical network(VON)acceptance ratio or network operator’s revenue.In[7],Chenet al.proposed an auxiliary graph based VONE scheme by coordinating VONs and a physical network to minimize the total network cost for a given set of VONs.In[8],Chowdhuryet al.proposed a node and link mapping formulation for the VONE problem to increase the acceptance ratio of VON services.They also developed two online VONE algorithms based on deterministic and random rounding techniques,respectively.Zhuet al.[9]proposed two VONE algorithms with defragmentation in both time and spectrum domains to improve the VON acceptance ratio in an EON.Jarray and Karmouch[10]formulated the VONE problem as a column generation(CG)based mathematical model and proposed a periodical auction based embedding process to maximize the network operator’s revenue.

In all the above studies,the VONE is assumed to be permanent and VONs cannot be changed once embedded.This,however,may not be efficient in practical scenarios with traffic fluctuations and network failures.To tackle this inefficiency,various approaches have also been considered in the literature,which are classified into three categories,i.e.,VON migration,VON reconfiguration,andVON resource sharing.

VON migrationmigrates certain elements (e.g.,virtual nodes,virtual links)in the VONs to better align resource allocation according to the current network status.In[11],Baiet al.proposed a reactive virtual node migration scheme for cloud-based VON services to reduce the VON request blocking probability and migration cost.Hsu and Shieh[12]proposed a heuristic VONE algorithm that enables path migration to migrate virtual links to different substrate paths,thereby maximizing the number of coexisting VONs in a substrate network and increasing the revenue of a network operator.By dynamically migrating both virtual nodes and links,Gao and Rouskas[13]proposed a migration scheme to balance the load on a substrate VON.In[14],Waniset al.proposed a proactive resource reoptimization technique that does both VON selection and migration to overcome fragmentation issue in the substrate network.Yuet al.[15]proposed a scheme that allows a substrate network to embed a virtual link over multiple substrate paths and employs path migration to periodically re-optimize the utilization of the substrate network.Caoet al.[16]proposed a reembedding scheme to re-embed virtual elements(i.e.,virtual nodes and links)for QoS-unguaranteed VONs.In[17],Meloet al.proposed an online VON reembedding formulation to migrate VONs away from physical resources with a high failure probability at a minimum overall migration cost.

VON reconfigurationachieves a better VONE solution by reconfiguring VONs.This may be classified intotopology reconfigurationandbandwidth reconfiguration.For topology reconfiguration,Tarutaniet al.[18]proposed a generalized flattened butterfly based VON reconfiguration scheme that reconfigures the topologies of VONs to reduce the energy consumption of a data center network.Tzanakakiet al.[19]proposed stochastic linear programming models for adaptive VON re-planning with uncertain traffic requests over optical networks and minimized the impact of this uncertainty on the availability,efficiency,and resilience of VONs.To reduce expenses while ensuring the QoS required,Moraleset al.[20]proposed a VON reconfiguration scheme to reconfigure VON topologies based on the predicted traffic obtained by a machine-learning algorithm.

For bandwidth reconfiguration,Hanet al.[21]proposed a VONE framework for QoS satisfaction and network reconfiguration.This enables adaptive bandwidth allocation and VON reconfiguration to maximize a network operator’s revenue.Dabet al.[22]proposed a genetic algorithm-based scheme for VON resource reconfiguration,which allocates VON resources according to users’dynamic requirements.By reallocating the resources of the VONs,the proposed scheme sequentially generates reconfiguration solutions that minimize both migration and embedding costs and eventually selects the best one.Miyazawaet al.[23]proposed a reinforcement learning based resource reconfiguration approach that selects and reallocates resources of non-urgent VONs automatically so as to satisfy QoS requirements dynamically.VON resource sharing aims to share allocated resources between accepted VONs.In[24],Oginoet al.proposed a priority queuing mechanism based VONE scheme that enables multiple virtual links traversing the same substrate link to share the bandwidth for minimizing the total required substrate resources.Zhanget al.[25]presented an opportunistic resource sharing based VONE framework,where substrate resources are opportunistically shared between multiple VONs to achieve an overall better VON acceptance ratio.

Many earlier studies have focused on accepting more VONs in a substrate network by reconfiguring provisioned VONs through virtual node/link migration(i.e.,by migrating the virtual nodes/links that are hindering provisioning of new VONs to other physical nodes/wavelength channels or physical paths).There are also studies attempting to modify the topologies and bandwidth required by new VONs.However,VON migration and reconfiguration based approaches require adequate idle network resources for establishing migrated or reconfigured VONs,i.e.,those that cannot be provided guaranteed QoS in scenarios where substrate resources are limited.Moreover,migration and topology reconfiguration based approaches may affect a group of virtual links associated with each other,which may lead to the issues of leveraging latency,operational overhead,and service interruption.Even in the approaches allowing for VON resource sharing,although spectrum utilization of accepted VONs can be relatively improved,the resource limitation in the former two categories may still exist and the fairness of resource sharing is a critical issue to be addressed.Although there have been some studies to consider the fairness in VON resource sharing using game theory based approaches[25],it is still difficult to achieve optimality (e.g.,equilibrium in noncooperative game)for some scenarios.

To tackle the above problems,based on the previous spectrum trading mechanism[5,6],we propose in this paper a novel three-stage SATP scheme that can provision QoS-guaranteed and cost-minimized VEON services in an EON.In addition to allocating spectrum resources to VEONs with given satisfaction ratios for reducing CAPEX,the proposed scheme allows VEONs to trade their spectrum resources with each other to maximize the utilization of the spectra that has been already allocated.The clients are not required to pay for using these traded resources but are motivated to do so for mutual benefit.Only when the bandwidth demands of VEONs still cannot be satisfied,additional spectrum resources would be purchased from the network operator to guarantee each VEON’s QoS.

The proposed SATP scheme is novel and more comprehensive than the conventional VEON reconfiguration where spectrum resources are simply reconfigured,increased or decreased,controlled by a network operator.In addition to spectrum allocation and reconfiguration in the different stages controlled by the network operator,our proposed scheme incorporates a stage to trade spectrum resources where the decisions of trading are made by VEON users,not by the network operator.Thus,the overall provisioning process requires significant additional effort than the conventional reconfiguration.

III.BASIC CONCEPTS

In a virtualized EON as shown in Figure 1,the infrastructure provider manages the substrate network,and the service provider maintains multiple VEONs on top of this by acquiring heterogeneous underlying resources(e.g.,bandwidth,computing resources,etc.)for clients with different service requirements.To reduce the cost paid by VEON clients while still providing guaranteed QoS on VEONs,we develop the SATP scheme for VEON service provisioning,which consists of the stages ofspectrum assignment,spectrum trading,andspectrum purchasing.

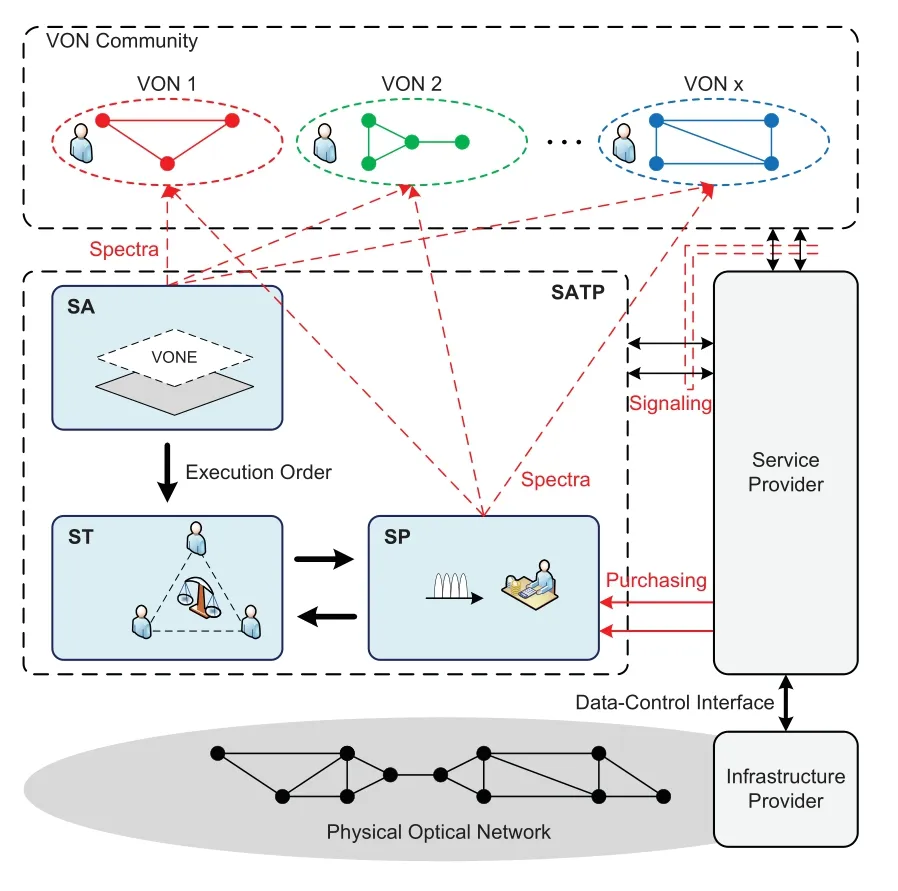
Figure 1. Illustration of the SATP scheme.

3.1 Spectrum Assignment

In this stage,the service provider receives and appropriately combines VEON requests from clients and implements VONE to allocate underlying resources according to the predicted bandwidth requirements based on a certain satisfaction ratioα(0＜α ≤1).Here satisfaction ratio means the percentage of traffic demand to be served in the SA stage for the predicted traffic demand.We assign different satisfaction ratiosαaccording to VEON clients’QoS requirements.For example,if a client has a higher priority,then we assign it with a larger satisfaction ratio such that it has more bandwidth to serve traffic demands.Based on the satisfaction ratio,the number of frequency slots(FSs)allocated to each virtual link at this stage is calculated as[26],whereZis the maximum traffic demand predicted on the virtual link,αis the satisfaction ratio of this predicted traffic demand,Bis the bandwidth allocated to an FS,andSErepresents the spectrum efficiency of the modulation format applied to establish the lightpath for the virtual link.Moreover,since the polarization division multiplexing technique is always applied,the data-rate carried by each FS is doubled.Spectrum resources allocated to each VEON in this stage are referred to asassigned spectra.By setting a proper satisfaction ratio,the cost of a VEON can be somewhat reduced,but it may then suffer from resource shortage when its traffic demand exceeds its allocated capacity.

3.2 Spectrum Trading

To address the resource shortage due to the limited spectrum resources assigned at the spectrum assignment stage,this stage allows different VEON clients that agree to join a VEON trading community to trade their spectrum resources according to their actual traffic demands.This stage is referred to as the spectrum trading stage.Specifically,whenever VEONs are short of spectrum resources in carrying their own traffic demands,they can obtain some unused spectrum resources from other VEONs by paying some trading credits[5,6].Here,the trading credit is defined to record the contribution that a VEON has made to the VEON community,i.e.,the spectrum resources that it has contributed to the community for other VEONs to use.Based on this,a cumulative credit can be further defined as the sum of trading credits paid or obtained by each VEON client during the service contract period,expressed aswheretis the index of the current time slot,andcv,jis the number of trading credits paid or obtained by VEON clientvin time slotj.To prevent selfish clients from abusing spectrum resources in the community,the ST scheme also defines a threshold for the cumulative credit of each VEON.When a VEON’s cumulative credit is smaller than a pre-set threshold,it is not allowed to acquire more spectrum resources from the community via spectrum trading until it has contributed sufficient spectrum resources to others.Aiming to form a mutually beneficial community where all VEON clients can benefit from such trading,we do not reward credit coins or other currencies for successful trading as some clients may abuse network resources by overdrawing their coins without proper supervision.Spectrum resources that a VEON obtains in this stage are calledtraded spectra.Through spectrum trading,more VEON traffic demands can be served and the unused spectrum resources on each VEON can be better utilized.However,even with the support of spectrum trading,it may not be possible to avoid service degradation of a VEON since the spectrum resources of the whole community are limited while the traffic demands on various VEONs may be higher.When the traffic demands on VEONs exceed the capacity provisioned for the whole community,there would be traffic loss and the VEON services would be degraded.

3.3 Spectrum Purchasing

To resolve the issue of spectrum shortage in the spectrum trading stage,this stage allows VEONs to purchase extra spectrum resources from their network operator(s) if their traffic demands can still not be fully served using the spectrum resources obtained for the whole community.Spectrum resources that a VEON obtains in this stage are calledpurchased spectra.Here,to minimize the cost paid by each VEON client,the spectrum resources purchased from the network operator are just sufficient to accommodate the excess traffic demands.

3.4 Summary

The purpose of the SATP scheme is to make use of the idle allocated resources when the traffic on a VEON surges in a VEON environment.There is only one VEON operator in this study,i.e.,the VEON operator owns the entire physical infrastructure of an EON.Since VEON users may not have global information on the substrate network,they need to monitor their own network resource usage,e.g.,how much has been used,how much remains idle,and how much more is required.With this information,they can then decide trading with other VON users or purchasing more resources from the network operator when the traded resources are not enough.After the trading or purchasing decision is made,the network is then configured by the operator.Though today it is still quite difficult to provision optical bandwidth in real time(e.g.,several minutes),the provisioning time has been significantly shortened from several weeks in the past to several hours today in some advanced optical networks.We expect that the provisioning time can be further shortened in the future with the maturity of software defined network (SDN)-enabled optical switch components and subsystems.

In the SATP scheme,VEON service provisioning is carried out on a time slot basis,and the lifetimes of all VEONs are divided into multiple equal time slots(TS).The SA stage is implemented at the beginning of the first TS,and the ST and SP stages are implemented starting from the beginning of each TS until the service contract of each VEON expires.Since it is implemented in a time-slotted manner,the SATP scheme is efficient when a relative long operational time slot is considered and/or the traffic variation follows a pattern such as tidal traffic where the peak and idle durations last for relatively long times.As long as the time slots are long enough,we can always benefit from the proposed scheme in improving spectrum efficiency when provisioning bandwidth for clients.In contrast,for traffic variations in short time slots,the proposed scheme may not be justified because frequent network reconfigurations can lead to much control overhead such as lightpath modifications and signaling messages exchanged,etc.

In this paper,we consider transparent VONE[27]where constraints such as spectrum continuity and contiguity are taken into account.Moreover,in the ST and SP stages,the sub-band virtual concatenation(VCAT)or spectrum splitting(SS)technique[28-31]is assumed for greater flexibility and better utilization of spectrum resources when provisioning VEONs.Specifically,this allows a virtual link to be established through an optical channel formed by multiple separate sub-bands that traverse different routes.

IV.PROBLEM STATEMENT AND MILP MODEL

In this section,we formulate the SATP process of VEON service provisioning as an optimization problem and develop an MILP optimization model to solve it.The VONE problem has been proven NP-hard[32].Therefore,the considered VEON service-provisioning problem is also NP-hard since it includes the VONE phase.

4.1 Problem Statement

We assume that an EON is denoted as{N,L},whereNis the set of physical nodes andLis the set of physical links.We also assume a set of VEONsV,each of which is denoted as{Ov,Gv}whereOvis the set of virtual nodes andGvis the set of virtual links in VEONv ∈V.Moreover,the set of all virtual nodes is denoted asE= ∪v∈V Ov(∪is the union operator) and the set of all virtual links is denoted asK= ∪v∈V Gv.Each virtual linkk ∈Kof the VEON has a traffic demandDkin each TS.In the SATP problem,we aim to minimize the overall cost paid by all the VEON clients.Here we focus on the cost paid for network resources (i.e.,fiber spectra),but do not consider the cost that may be paid for computing and storage resources on virtual nodes.The proposed service provisioning scheme can also be extended to consider computing and storage resources on virtual nodes (e.g.,cloud resources) when provisioning a VEON.Under these circumstances,in addition to the constraints for bandwidth resources,i.e.,spectrum continuity and contiguity,the constraints for cloud resources should also be considered to ensure that the provisioned cloud resources do not exceed the total available cloud resources.On the other hand,since all the VEON clients have formed a cooperative community,we do not count the cost of spectra traded between VEON clients in the ST stage,but do include the costs of the spectra obtained from the network operator in the SA and SP stages.For simplicity,we assume that the cost of spectrum is 1 unit/FS/TS although it may also be related to the length of a virtual link.

As mentioned earlier,the SATP scheme is considered on a time slot basis.The SA stage is implemented at the beginning of the first TS while the ST and SP stages are implemented at the beginning of each subsequent TS until the service contract of each VEON expires.We only formulate ST and SP jointly in the following MILP model,while implementing SA using a heuristic algorithm described in the next section.It is noted that the SA phase can also be done optimally with MILP,which would further improve the performance of the proposed scheme.However,this will make the model extremely complicated even for a small testing scenario.On the other hand,the heuristic algorithm employed for the SA phase in this study has been verified in the literature to be almost as efficient as the MILP model.Therefore,we employ the heuristic algorithm for the SA phase,and do not consider an MILP model jointly incorporated with the SA phase.

4.2 MILP Model of Joint ST and SP

The MILP model of joint ST and SP is presented as follows.For simplicity,we useto represent the set of integers{a,...,b}.

Sets:

L,Set of physical links.

V,Set of VEONs.

K,Set of virtual links.

Gv,Set of virtual links belonging to a VEONv ∈V,

Gv ?K.

Ik,Set of physical links that a virtual linkk ∈Ktraverses,Ik ?L.

Parameters:

T,An integer parameter that denotes the number of time slots.

F,An integer parameter that denotes the number of FSs on each physical link.In this paper,we assume adequate spectra and therefore setFto be a large value.

S,An integer parameter that denotes the maximum number of VCAT sub-bands that can be used for establishing a virtual link.

W,A parameter that denotes the threshold of cumulative credit for each VEON client.

Dk,t,A parameter that denotes the traffic demand (in units of Gb/s)on a virtual linkk ∈Kin.B,A parameter that denotes the bandwidth allocated to each FS(in units of GHz).In this paper,we assumeBto be 12.5 GHz.

SEk,A parameter that denotes the spectrum efficiency(in units of bit/s/Hz) of the most efficient modulation format that can be used to establish the lightpath corresponding to a virtual linkk ∈K.

M,An integer parameter that denotes a large value.In this paper,we setMto be 104.

ε,A parameter that denotes a small value.In this paper,we setεto be 10-4.

∈,A parameter that denotes the weight of an objective.In this paper,we set∈to be 0.1.

Variables:

Fmax,An integer variable denoting the maximum index of FS used.

cv,t,A variable that denotes the credit paid or obtained by VEONv ∈Vin.

ζv,t,A binary variable that equals 1 if the cumulative credit of VEONv ∈Vis smaller than a pre-set thresholdWin;0,otherwise.

δk,t,A binary variable that equals 1 if the spectra of virtual linkk ∈Kis not enough to accommodate its traffic in;0,otherwise.

φk,s,t,A binary variable that equals 1 if virtual linkk ∈Kuses sub-bandin;0,otherwise.

xk,s,t,An integer variable that denotes the starting FS index of sub-bandof virtual linkk ∈Kin TS.

yk,s,t,An integer variable that denotes the ending FS index of sub-bandof virtual linkk ∈Kin TS.

bwk,s,t,A variable that denotes the bandwidth(in units of GHz)provided by sub-bandof virtual linkk ∈Kin TS.A binary variable that equals 1 if thes-th (s ∈sub-band of virtual linkk ∈ Koccupies FSon physical linkl ∈Lin TS; 0,otherwise.

Objective:minimize

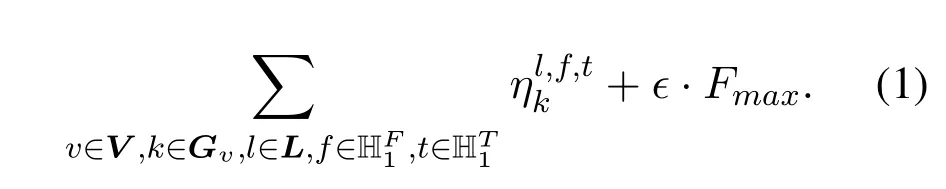
The first objective is to minimize the total cost paid by all the VEONs and the second objective is to minimize the maximum index of FS used.

ST permission-related constraints:

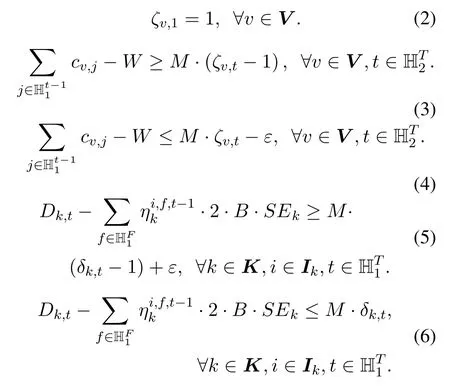
Constraint(2)ensures that all VEON clients are eligible for SATP in the first time slot.Constraints(3)and(4) ensure that if the cumulative credit of a VEON is not smaller than a pre-set threshold,then it is eligible for spectrum trading(i.e.,ζv,t=1);otherwise,it is not eligible(i.e.,ζv,t= 0).Constraints(5)and(6)ensure that a virtual link requires extra spectra(i.e.,δk,t=1)if the spectra that it owns are not enough to serve its traffic demand.

VCAT sub-band related constraints:

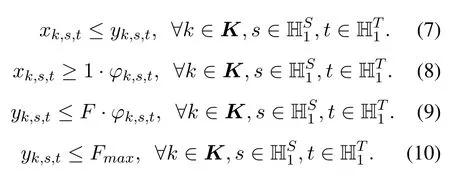
Constraint (7) ensures that the starting FS index of a sub-band is not larger than its ending FS index.Constraints (8) and (9) ensure that if a sub-band is used to established a virtual link (i.e.,φk,s,t= 1),then its starting and ending FS indexes are within the range of[1,F]; otherwise,they equal zero (i.e.,xk,s,t=yk,s,t=0).Constraint(10)ensures that the ending FS index of a sub-band is not larger than the maximum index of FS used.

Spectrum-related constraints:

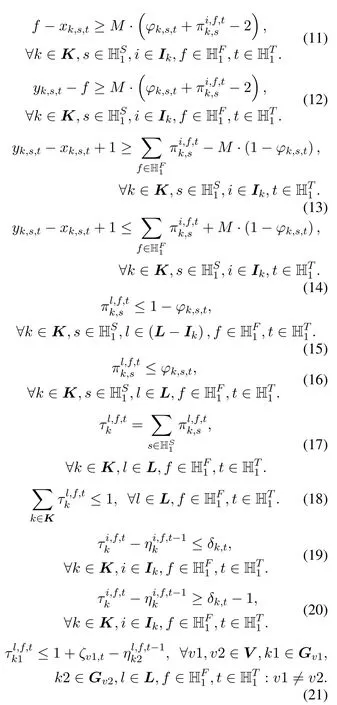
Constraints (11) and (12) ensure that if an FS is not within a sub-band (i.e.,f /∈[xk,s,t,yk,s,t]),then it is not occupied by the corresponding virtual link of the sub-bandTogether with constraints(11) and (12),constraints (13) and (14) ensure that all FSs within a sub-band (i.e.,f ∈[xk,s,t,yk,s,t])are occupied by its corresponding virtual link (i.e.,Constraints(11)-(14)are valid only if the sub-band is used to establish the virtual link on one of its candidate routes (i.e.,φk,s,t= 1).Constraints(15)and(16)ensure that a sub-band does not occupy FSs on physical links that it does not traverse.Constraints (17) and (18) ensure that an FS can be occupied by at most one sub-band of a virtual link.On the other hand,they can ensure that the spectra of each two sub-bands do not overlap(i.e.,non-overlapping spectrum).Constraint (19) ensures that,if a virtual link does not require extra spectra (i.e.,δk,t= 0),then it can only occupy its own FSs,originally assigned in the SA stageConstraint (20)ensures that if a virtual link requires extra spectra(i.e.,δk,t= 1),then all its own FSs should be used firstConstraint (21) ensures that if a VEON is not eligible for spectrum trading (i.e.,ζk1,t= 0),then it cannot obtain spectra from others.

Bandwidth-related constraints:

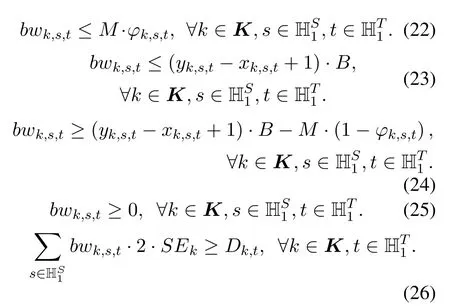
Constraints(22)-(25)ensure that if a sub-band is used to establish a virtual link (i.e.,φk,s,t= 1),then its bandwidth is the product of the number of its FSs and the bandwidth of each FS (i.e.,bwk,s,t=(yk,s,t ?xk,s,t+1)·B); otherwise,its bandwidth equals zero(i.e.,bwk,s,t=0).Constraint(26)ensures that the total bandwidth of all sub-bands used to establish a virtual link is not smaller than the total traffic demand(at the level of QoS required)on it.

Cost-related constraints:

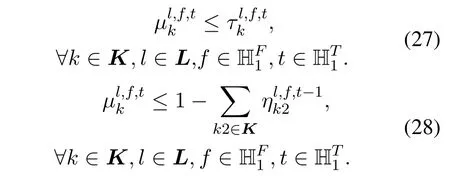
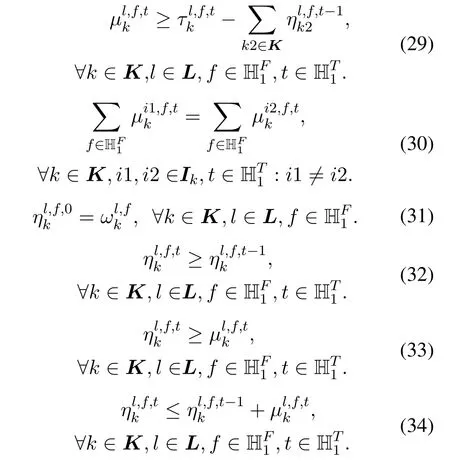
Constraints (27)-(29) ensure that if a FS is occupied by a virtual linkbut does not belong to any virtual link then it must be newly purchased in the SP stage(i.e.,Here,the AND operations converted into linear constraints.Constraint (30) ensures that the newly purchased spectra on all virtual links along a physical route should be of equal amounts.This constraint is to prohibit a virtual link from serving its traffic demand by mixing up the traded spectra obtained in the ST stage and the purchased spectra obtained in the SP stage.Because the traded spectra may be occupied by other virtual links in the following TSs,this would make the purchased spectra unusable (limited by spectrum continuity).Constraint(31)ensures that the spectra belonging to a virtual link in time slot T0 are those allocated to the virtual link in the SA stage.Constraints(32)-(34)ensure that the spectra currently assigned to a virtual link is the sum of its own spectra in the SA stage and newly purchased spectra in the SP stage.Here,the OR operationis converted into linear constraints.

Credit-related constraints:

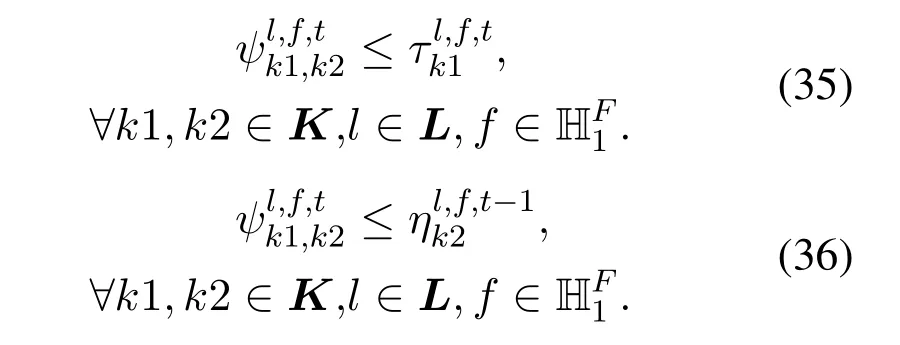
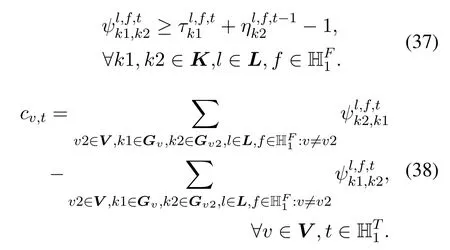
Constraints(35)-(37)ensure that if a virtual link uses spectrum owned by another virtual link,then1.Here,the AND operationis converted into linear constraints.Constraint (38)ensures that the increase/decrease of the credit of a VEON is equal to the number of FSs that it trades to/from other VEON clients.The part before the minus sign denotes the total number of FSs that VEONvtrades to others and the part after the minus sign denotes the total number of FSs that VEONvobtains from others through trading.

4.3 Complexity of the MILP Model of Joint ST and SP

The computational complexity of an MILP model is decided by the dominant numbers of variables and constraints[33].For the MILP model of joint ST and SP,the dominant number of variables is decided by variablewhich is at the level ofHere|K|is the total number of virtual links in all VEONs,|L|is the total number of physical links,Fis the total number of FSs in each physical link,andTis the total number of time slots.Similarly,the dominant numbers of constraints are also at the level ofdue to constraints(35)-(37).

V.HEURISTIC ALGORITHMS

For large-scale network scenarios,the above MILP model cannot obtain optimal solutions within a reasonably short time.Therefore,we also develop efficient heuristic algorithms for each stage in the SATP scheme.Since the heuristic algorithm in[6]is adopted for the ST stage,we only present the heuristic algorithms for the SA and SP stages next.

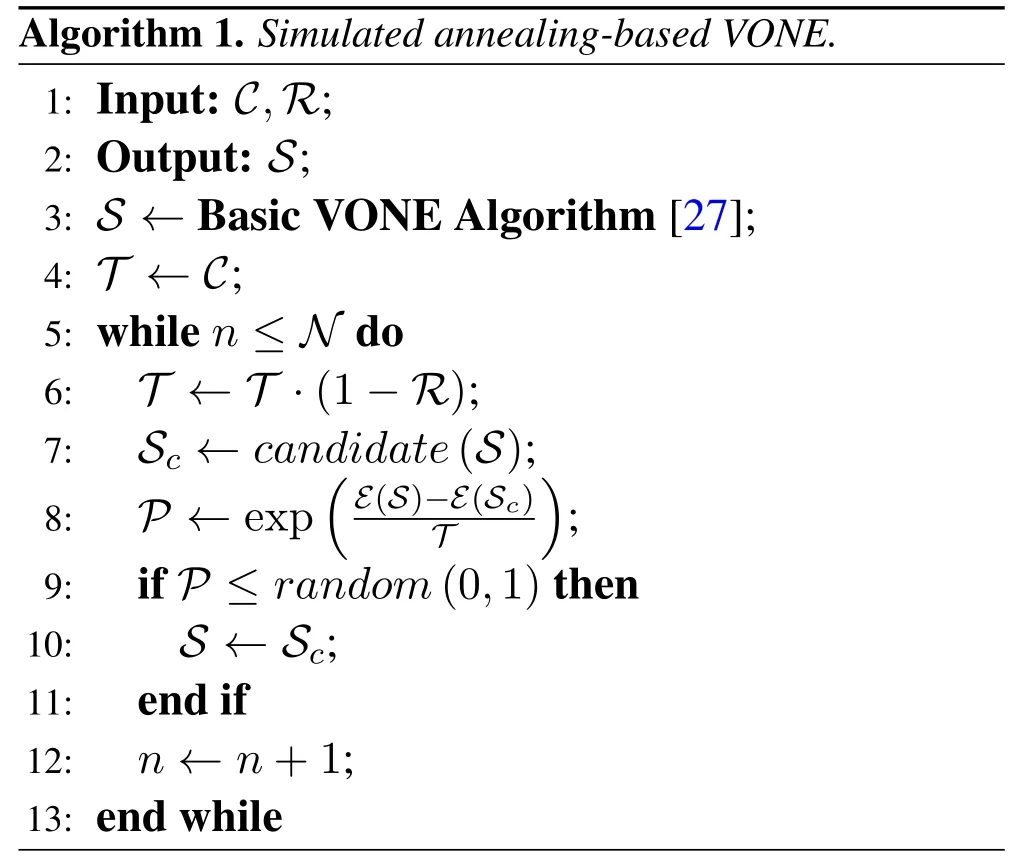
Algorithm 1.Simulated annealing-based VONE.1:Input: C,R;2:Output: S;3: S ←Basic VONE Algorithm[27];4: T ←C;5:while n ≤N do 6: T ←T ·(1 ?R);7: Sc ←candidate(S);8: P ←expimages/BZ_165_1585_790_1612_836.pngE(S)-E(Sc)images/BZ_165_1803_790_1830_836.pngT ;9:if P ≤random(0,1)then 10:S ←Sc;11:end if 12: n ←n+1;13:end while

5.1 Heuristic Algorithm of SA

We use a simulated annealing based VONE algorithm[34]to assign spectra to the VEONs in the SA stage.The pseudocode is presented in Algorithm 1.First,we map VEONs onto the physical network using the basic VONE algorithm in[27]and consider the embedding state as the current VONE stateS.Then,we cool down the temperatureT(initial temperatureC) with a cooling rateRand generate a candidate VONE stateScby migrating a virtual node’s mapping location onto different physical nodes using functioncandidate(S).Since a changed mapping location of a virtual node would change the physical routes that its associated virtual links traverse and consequently impact the whole VONE solution,we remap all VEONs for a candidate solution after virtual node migration.Next,with the current temperatureTand the energies of the current and candidate VONE statesE(S) andE(Sc) (in this paper,the maximum index of FS used is considered as the energy of a VONE state),we generate an acceptance probabilityP.If the acceptance probability is not smaller than a randomly generated probabilityrandom(0,1),then we accept the candidate VONE stateSc.After that,we repeat procedures from Line 6 to Line 11 until a maximum ofNsteps have been taken.

In the above simulated annealing-based VONE algorithm,the solution of the VONE problem moves to a candidate solution in each iteration with a temperature-related probability.With decreasing temperature,the algorithm has less chance to move to a worse solution after an iteration.When the temperature gets very close to 0,only a better solution can be accepted,which ensures that the algorithm can finally converge.

Algorithm 2.Spectrum purchasing.1:Input: K,{pk}k∈K,{F′k}k∈K,Fmax;2:Output:Purchasing info,{$v}v∈V ,Fmax;3: K ←sort(K,F′);4:for each virtual link k in K do 5:while F′k ＞0 do 6:Ω ←createSW (pk,F′k,Fmax);7:for each SW ω in Ω do 8:if SW ω is available then 9:purchase;10:$v ←$v+F′k·hk;11:if Feω ＞Fmax then 12:Fmax ←Feω;13:end if 14:break while;15:end if 16:end for 17:Fmax ←Fmax+1;18:end while 19:end for

5.2 Heuristic Algorithm of SP

In the SP stage,the VEON clients with unserved traffic demands can purchase additional spectra from a network operator.Specifically,the clients request extrarequired spectra along the physical route that it traverses and then the new purchased spectra are combined with its originally owned spectra into a superchannel for traffic delivery.The pseudocode of the heuristic algorithm of SP is given in Algorithm 2.First,we sort all virtual links in setKin descending order based on their unserved traffic demandsF′(in units of FSs) using functionsort(K,F′).Next,for each virtual linkkin the sorted setKthat requires additional spectrawe create spectrum windows (SWs)[35,36]withFSs whose indexes are smaller thanFmaxalong the shortest physical routepk(the physical route that a virtual link travers in the SP stage is the same one in the SA stage,i.e.,the shortest route) using functioncreateSWThen we check the availability of these SWs.If no available SW can be found,then we increase the maximum index of FS used by 1(i.e.,Fmax=Fmax+1)and repeat the same process.If an available SW is found,then we purchase the corresponding spectra for the virtual linkkand update the cost paid by the VEON bywherehkrepresents the number of hops in the route that virtual linkktraverses.Moreover,if the ending FS index of the selected SW,i.e.,,is larger thanFmax,then we assign the value oftoFmax.After that,we move to the next virtual link and repeat the above procedures until all the virtual links inKhave been traversed.

5.3 Complexity of Heuristic Algorithms

The computational complexities of the heuristic algorithms are analyzed as follows.For the heuristic algorithm of the simulated annealing based VONE,its computational complexity isNtimes of the applied basic VONE algorithm[27]whereNis the total rounds of simulated annealing.For the heuristic algorithm of spectrum purchasing,the computational complexity is at the level ofwhere|K|is the total number of all virtual links,Fmaxis the maximum number of unused FSs,andis the maximum number of extra-required FSs of virtual links in the SP stage.

VI.TEST CONDITIONS AND PERFORMANCE ANALYSIS

We conducted extensive simulations under both static and dynamic traffic demand scenarios to evaluate the performance of the proposed SATP scheme.In the static scenario,all VEON requests are assumed to be known in advance.In the dynamic scenario,the VEON request arrival follows a Poisson distribution and the service duration follows an exponential distribution.Under the static scenario,we considered the total cost paid by VEON clients and the maximum index of FS used as the performance evaluation metrics.Under the dynamic scenario,we considered the VEON blocking probability and total lost traffic in the served VEONs as the performance evaluation metrics.

6.1 Test Conditions

To evaluate the performance of the SATP scheme,we conduct simulations based on a 6-node,8-link n6s8 network,the 11-node,26-link COST239 network,and the 14-node,21-link NSFNET network as shown in Figure 2.Three modulation formats(MFs),i.e.,BPSK,QPSK,and 8-QAM,are chosen for setting up virtual links based on their physical distances.The transparent reaches and data rates of different modulation formats are given in Table 1[26].

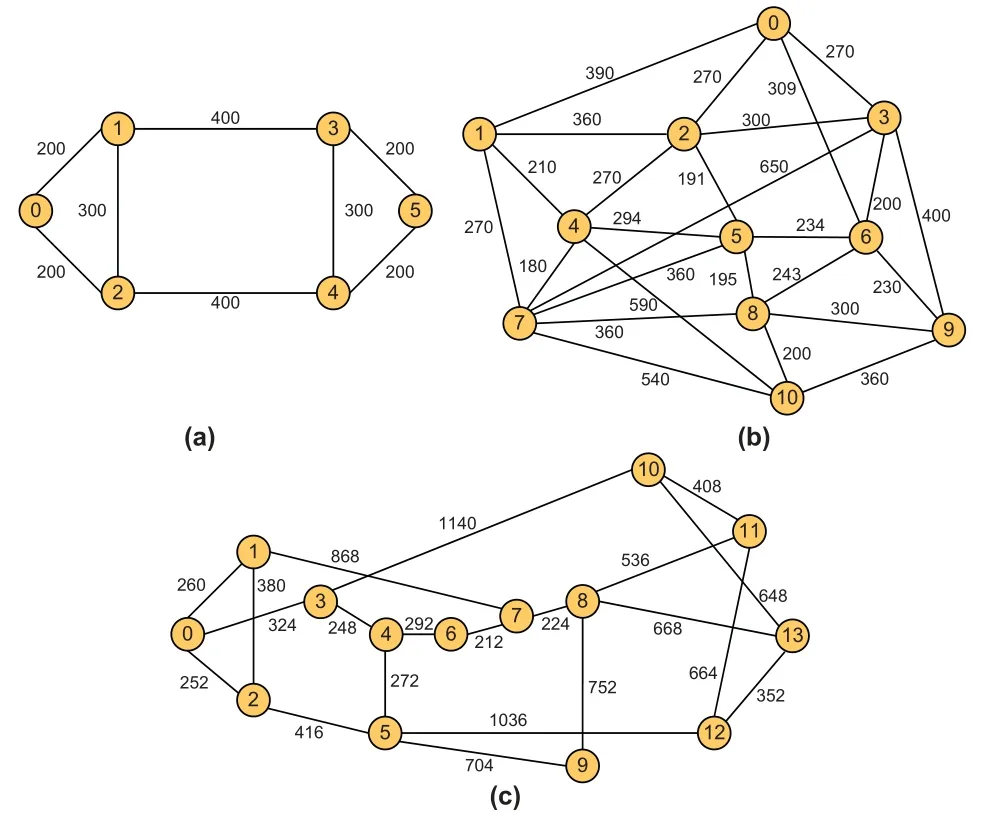
Figure 2. Test networks:(a) n6s8 network,(b) COST239 network;(c)NSFNET network.

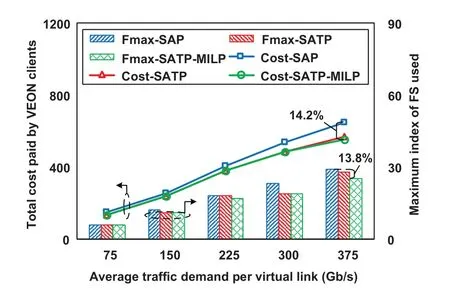
Figure 3. Performance comparison under different average traffic demands per virtual link in the n6s8 network.

For the static scenario considered in the n6s8 network,we assume that there are 4 VEONs,each of which hasO ∈{3,4}virtual nodes andG ∈[O ?1,O·(O ?1)/2]virtual links.The lifetime of the VEONs is divided into four TSs.The average traffic demand on each virtual link isAGb/s,whereAis randomly selected from set{75,150,225,300,375}Gb/s.The actual traffic demand on each virtual link in each TS is randomly generated within the range ofD ∈(A·(1?γ),A·(1+γ)]Gb/s,whereγ(0＜γ ≤1) is the fluctuation level.FSs assigned to each virtual link in the SA stage is calculated bywhereα(0＜α ≤1) is the satisfaction ratio,Bis the bandwidth assigned to an FS(i.e.,12.5 GHz in this paper),andSEis the spectrum efficiency of the modulation format selected from Table 1.The cost of the spectrum obtained from the network operator is set to be 1 unit/FS/TS.The threshold of the cumulative credit is set to beW=?6,which means that if the cumulative credit of a VEON is smaller than -6,then it cannot acquire any spectrum resources from the trading community.Note that such a threshold is set according to the observation in our previous study[6],where a saturation trend is observed between the cumulative credit threshold and the system performance.Specifically,when the threshold changes within the range of[?8,?4],the network performance will not significantly change with the further reduction of the threshold[6].Thus,we set this threshold to be-6 in this study.The number of VCAT sub-bands supported is 4.For the simulated annealing based VONE algorithm,the initial temperature is set to beC=106,the cooling rate is set to beR=10-4,and the maximum number of simulated annealing rounds is set to beN= 105.For the large networks (i.e.,COST239 and NSFNET),we assume that there are 20 VEONs and all the other settings are the same as in the n6s8 network.

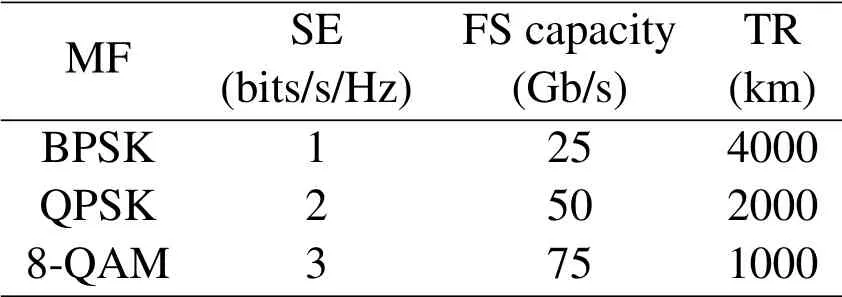
Table 1. FS capacities and transparent reaches (TRs) of different modulation formats(MFs).

In the following simulations,without explicit indication,the average traffic demand on each virtual link is set to be 375 Gb/s,the satisfaction ratio in the SA stage is set to beα=0.5,and the level of traffic fluctuation on each VEON is set to beγ=1.0.In addition,because the sequence of VEON requests shows an impact on the performance of the proposed scheme,we run our MILP model and heuristic algorithms 10 times to get their averages.

In the proposed VON provisioning scheme,the spectrum assignment phase can be done with any existing VONE algorithms.The spectrum trading and spectrum purchasing phases are carried out based on the outcome of the spectrum assignment phase (i.e.,the VONE phase) to achieve performance improvement.In this case,the proposed approach can always outperform the basic VONE.Therefore,we do not compare the proposed approach with other existing VONE algorithms.Moreover,because there are no studies on spectrum trading and spectrum purchasing in the literature except those from our team,it is not possible for us to compare this work with others.However,to evaluate the performance of the proposed approaches and heuristic algorithms,we have compared the results of the MILP models and the heuristic algorithms to verify the efficiency of the latter.In addition,we also particularly consider the cases with only spectrum trading and spectrum purchasing as our benchmark schemes,denoted as SAT and SAP,respectively.However,SAT is only considered for the dynamic scenario.This is because in the static scenario,all traffic demands exceeding the allocated bandwidth would be discarded,which unfairly enables SAT to always outperform all the other cases in the performance perspectives of“Total cost paid by VEON clients”and“Maximum index of FS used.”

Before carrying out performance analyses for the different schemes,we define the following legends.Legend“SATP”represents the SATP scheme.Legend“SAP”represents the scheme without spectrum trading.Legend“SAT”represents the scheme without spectrum purchasing.Legend“MILP”represents the result of the MILP model,and the cases without this legend correspond to the heuristic algorithms.Legends“Cost”and“Fmax”in the static scenario represent the total cost paid by all VEON clients and the maximum index of FS used,respectively.Legends“BP”and“LT”in the dynamic scenario represent VEON blocking probability and total traffic lost,respectively.For example,“Cost-SATP-MILP”represents the total cost paid by all VEON clients obtained by the MILP model of the SATP scheme.

We employed the commercial AMPL/Gurobi software package(version 8.1.0)to solve the MILP model,which was run on a 64-bit server with 2.1-GHz CPU and 64-GB RAM.The MIPGAP for solving the MILP model was set to be 0.01%.The times taken for solving the MILP model in the three test networks were all within 2 hours.We implemented the heuristic algorithms using JAVA,which was run on a 64-bit computer with a 3.4-GHz CPU and 8-GB RAM.

6.2 Static Scenario

6.2.1 Performance comparison under different traffic demands

Figure 3 shows the performance of the SATP scheme in comparison with the benchmark scheme under different traffic demands on each virtual link in the n6s8 network.We can see that,with an increasing average traffic demand on each virtual link,the overall costs paid by the VEONs in both SATP and the benchmark scheme increase.This is because a higher average traffic demand corresponds to a wider traffic varying range,which would allow more opportunities to improve spectrum utilization by spectrum trading.Moreover,the SATP scheme can significantly reduce both the total cost paid by VEONs and the maximum index of FS used (Fmax) compared to the benchmark scheme (i.e.,SAP) by up to 14.2% and 13.8%,respectively.This is because SATP enables VEONs to acquire unused spectrum resources from the trading community at no extra cost instead of having to purchase additional spectra from a network operator whenever it lacks spectrum resources.

We also conducted similar simulation studies for the COST239 and NSFNET networks.Since the MILP model cannot obtain a result in a reasonable short time for large networks,we only show the results of the heuristic algorithm here.Figure 4(a)shows the results for the COST239 network.Similar to the results of the n6s8 network,we can see that,with increasing average traffic demand per virtual link,the overall costs paid by the VEONs in both the SATP and the benchmark schemes also increase.As before,SATP significantly reduces both the overall cost paid and Fmax compared to the benchmark scheme by up to 11.2%and 9.9%,respectively.Figure 4(b) shows the corresponding results for the NSFNET network which are also similar in nature.For this network,we see that up to 11.7%cost and 9.1%FSs can be saved when the SATP scheme is implemented,as compared with the benchmark scheme.

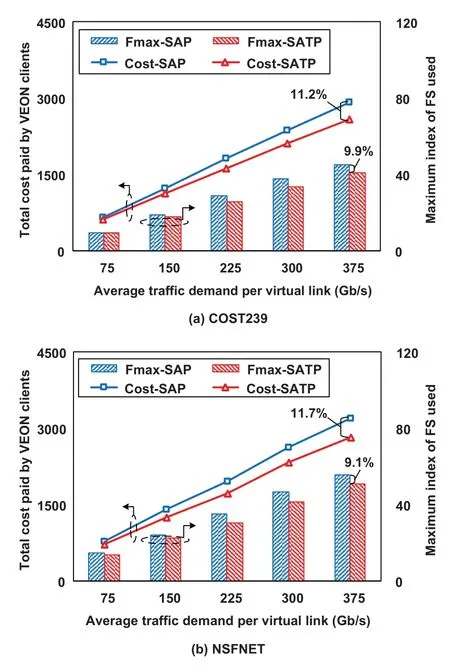
Figure 4. Performance comparison under different average traffic demands per virtual link in the large networks.

6.2.2 Impact of satisfaction ratio

To evaluate the impact of the satisfaction ratioαin SA on the performance of the SATP scheme,we conducted simulations for the COST239 and NSFNET networks.Figure 5(a) shows the results for the COST239 network.We can see that,for the SATP case,with an increasing satisfaction ratio in the SA stage,the total cost paid by the VEON clients decreases at first.This is because a smaller satisfaction ratio in the SA stage corresponds to fewer FSs allocated to VEONs,which reduces the opportunity of spectrum trading and therefore weakens the benefit of the ST process.When the satisfaction ratio becomes 0.5,the total cost paid by VEON clients is the minimum,and up to 11.2%cost and 9.9%FSs can be saved,respectively,compared to the SAP case.However,in contrast to this decreasing trend,when the satisfaction ratio increases further,the total cost tends to increase once again.This is because more FSs are allocated to the VEONs in the SA stage,some of which will probably never be used.When the satisfaction ratio becomes 0.9,the total costs paid by VEONs for the SATP and SAP cases are very close to each other.This is because the FSs allocated in the SA stage have been mostly enough to accommodate all user traffic,and therefore,the ST process is seldom triggered and less cost is saved by the SATP case.

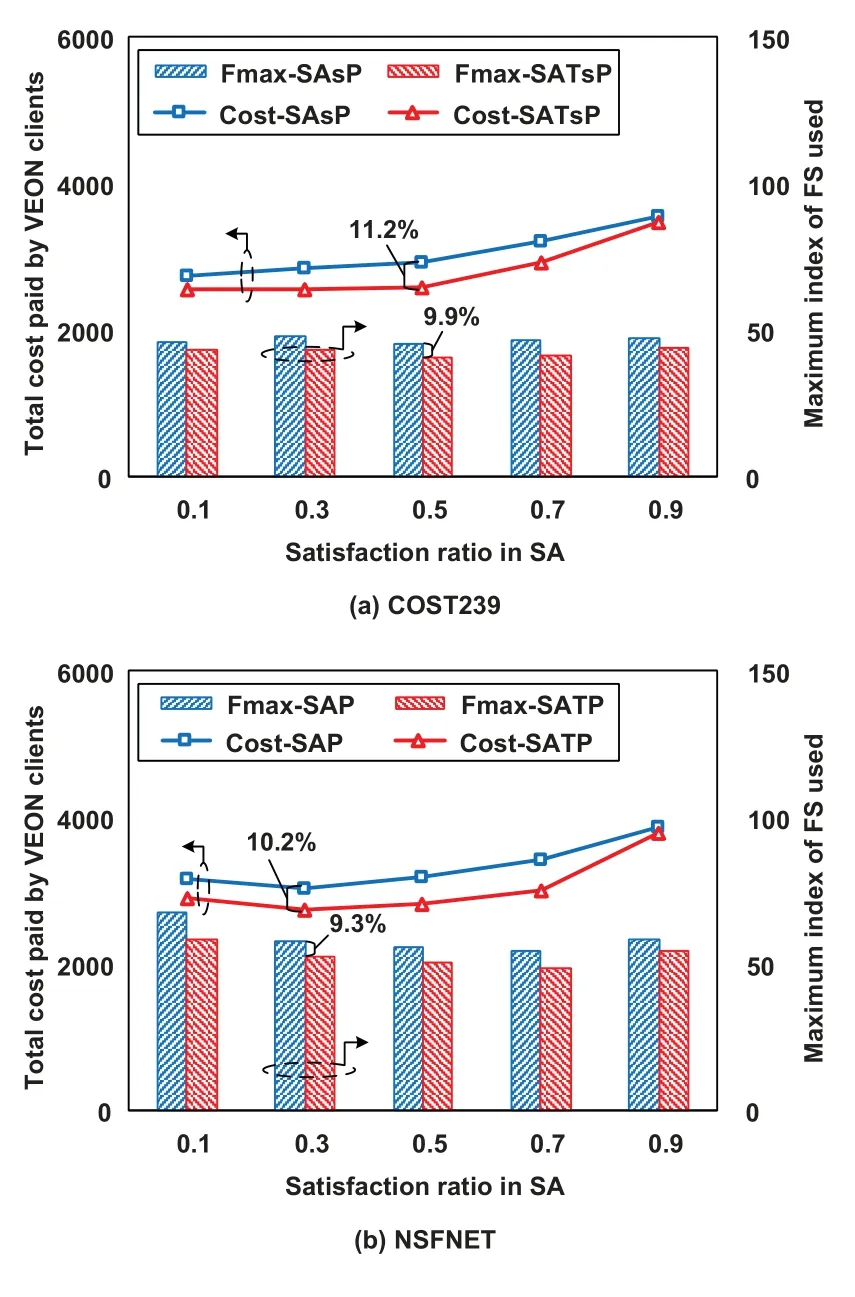
Figure 5. Impact of the satisfaction ratio α on the SATP performance in the large networks.

Figure 5(b)shows the results for the NSFNET network.It is found that the performance trend here is similar to that for the COST239 network.The only difference is that,in the NSFNET network,the“turning point”occurs when the satisfaction ratio is 0.3.(Recall that this was 0.5 for the COST239 network.)At this point,up to 10.2% cost and 9.3% FSs can be saved by the SATP scheme compared to the SAP case.

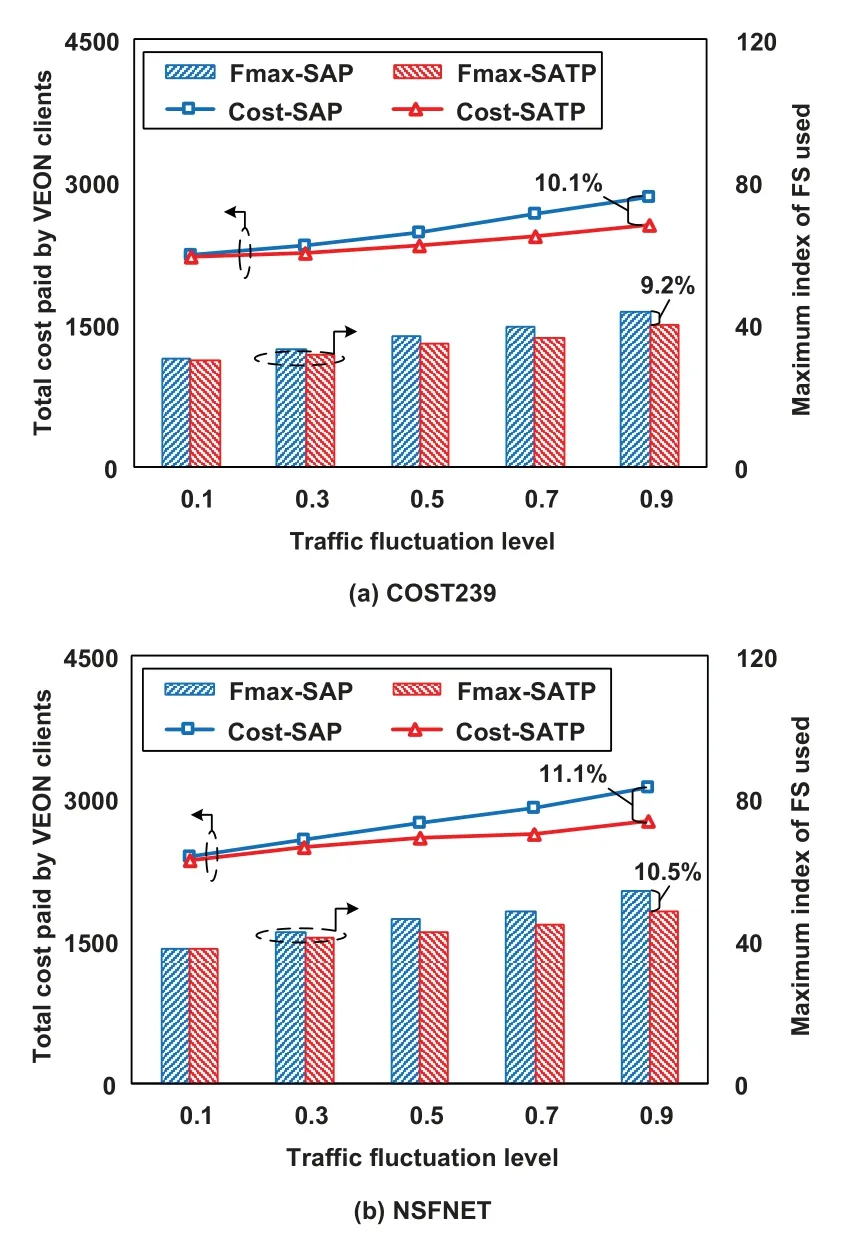
Figure 6. Impact of the traffic fluctuation level γ on the SATP performance in the large networks.

6.2.3 Impact of traffic fluctuation level

We also investigate the impact of the traffic fluctuation levelγon the performance of the SATP scheme in the COST239 and NSFNET networks.Figure 6(a)shows the results for the COST 239 network.We can see that with increasing levels of traffic fluctuation,the total costs paid by VEONs also increase.This is because the peak traffic demand of a VEON with a larger fluctuation level requires the VEON to purchase more spectrum resources from a network operator to accommodate all the traffic demand.In addition,more cost can be saved by SATP with increasing levels of traffic fluctuation.This is because a larger traffic fluctuation level corresponds to a larger difference between the actual traffic demands of a VEON and the spectra that it owns.In other words,more FSs remain idle on some virtual links and more FSs are required on other virtual links.Under this circumstance,more traffic demands can be established through spectrum trading.When the traffic fluctuation level becomes 0.9,up to 10.1%cost paid by VEONs and up to 9.2%FSs can be saved by the SATP scheme compared to the SAP case.

Figure 6(b)shows the results for the NSFNET network.We can see that with increasing traffic fluctuation levels,the total costs paid by VEONs increase and more cost can be saved by SATP for the same reason as for the COST239 network.When the traffic fluctuation level is 0.9,up to 11.1%cost and 10.5%FSs can be saved by the SATP scheme compared with the SAP case.

6.3 Dynamic Scenario

We also consider the SATP scheme in dynamic traffic demand scenarios,under which VEON requests arrive randomly and sequentially.The arrival instants and service durations of the VEON requests are not known in advance.We assume that VEON requests arrive following a Poisson process with an arrival rateλand the duration of each VEON service follows an exponential distribution with mean 1/μ.We set the mean duration 1/μof all VEON requests to be 4 TSs,e.g.,1/μ= 4.Total 1000 VEON requests were simulated.The average traffic demand per virtual link is 375 Gb/s and the level of traffic fluctuation on a VEON is set to beγ= 1.0.We also assume 120 FSs in each physical link.Note that the basic VONE algorithm is applied in the SA stage for the dynamic scenario.A VEON is considered served only if enough spectrum resources are assigned to meet its required satisfication ratio.

6.3.1 Performance comparison under different traffic loads

The performance comparison between the cases of SAT,SAP,and SATP under different VEON arrival rates in the three test networks are shown in Figure 7.We can see that SATP can outperform SAP in both VEON blocking probability and total traffic lost by VEONs in all the test networks.This is because spectrum trading enables a VEON that is short of bandwidth to obtain more bandwidth through trading,thereby reducing the VEON blocking probability.

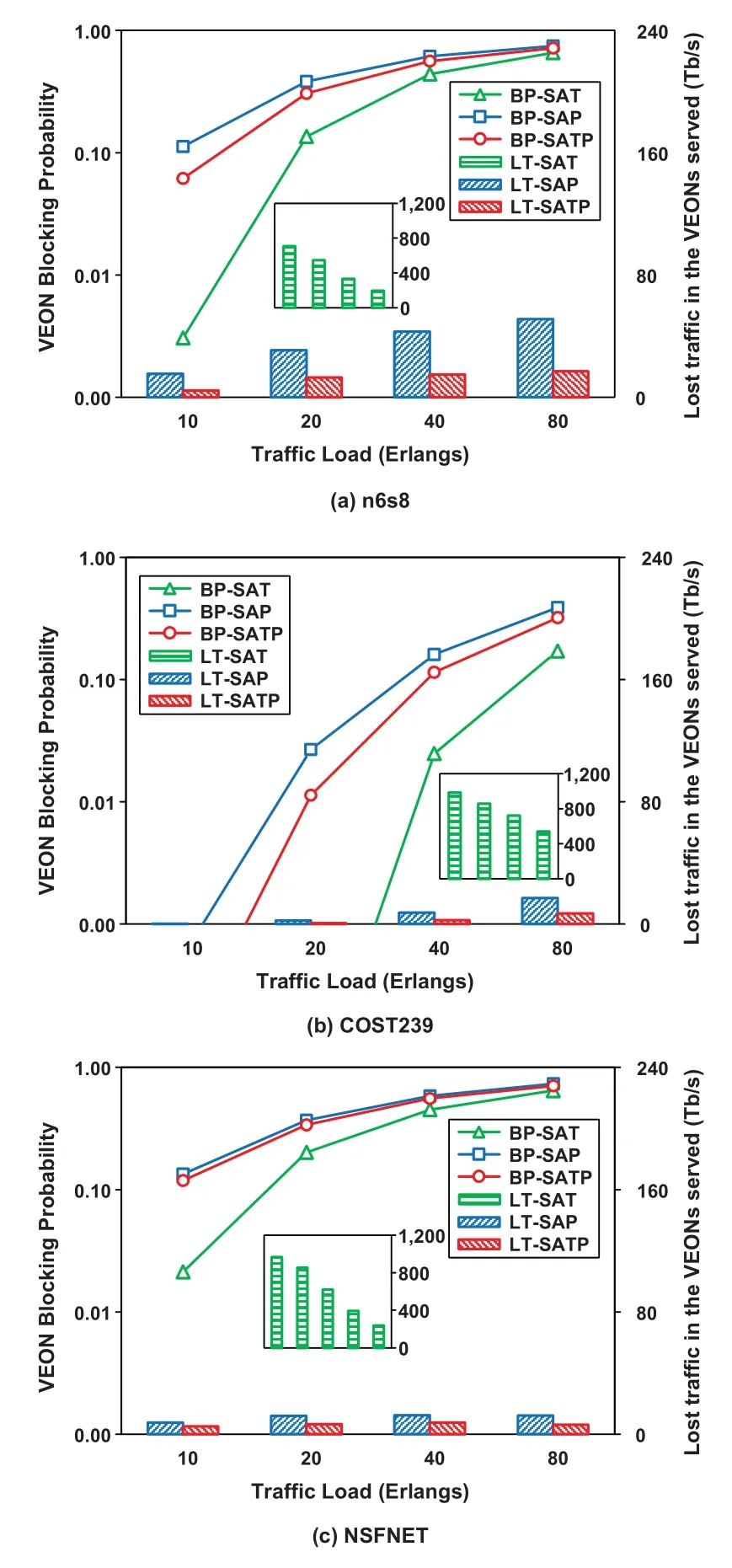
Figure 7. Performance comparison under different traffic loads in the three test networks.

SAT outperforms SAP and SATP in VEON blocking probability,but it suffers from more traffic lost by VEONs.This is because not allowed for spectrum purchasing,SAT must reject all traffic demands that cannot be carried after spectrum trading,and therefore,more traffic is lost in VEONs.On the other hand,as a return of more rejections,there are more network resources remained for provisioning new VEONs.Therefore,SAT shows a better performance in VEON blocking probability.

Also,under different VEON arrival rates,the results of the three test networks demonstrate the same trend.Specifically,with increasing traffic loads,the VEON blocking probabilities increase in all the test networks.However,for traffic lost by VEONs,SAT and the cases of SAP and SATP demonstrate opposite performance trends.SAT shows a trend of decreased traffic lost with the increase of traffic load,while SAP and SATP show trends of increased traffic lost.This is because we set the satisfaction ratio in the SA stage to be 0.5,so even under a small traffic load,SAT has a large amount of traffic lost although allowing spectrum trading.In contrast,allowing spectrum purchasing,SAP and SATP can always carry more users’traffic by purchasing more network resources.However,when the traffic load is high enough,spectrum resources remained in the network and allowed for purchase become very limited,which eventually becomes a bottleneck to carry more exceeded traffic.Thus,the amount of lost traffic also increases.

The specific performance values are also different for the three networks.For example,when the arrival ratio is 10 Erlangs,the VEON blocking probabilities in the n6s8 network are near 0.003,0.1,and 0.06,in the SAT,SAP,and SATP cases,respectively,as shown in Figure 7(a).However,in the COST239 network,the VEON blocking probabilities in all the three cases,as shown in Figure 7(b),are much smaller than 0.01(not shown,given the axis bounds).This is because the COST239 network has a larger topology and a higher node degree than the n6s8 network.Moreover,in the NSFNET networks,the VEON blocking probabilities in all the three cases are larger than 0.01 and the difference between SATP and SAP is much smaller(see Figure 7(c)).This is because the NSFNET network has a lower nodal degree than the n6s8 network even though it has a larger topology.With the same reason,we can see that less traffic is lost in the COST239 network in both SATP and SAP cases compared with the n6s8 and NSFNET networks.However,for SAT,not allowing spectrum purchasing is still the major reason for the traffic lost.

6.3.2 Impact of satisfaction ratio

To evaluate the impact of the satisfaction ratioαof SA on network performance,we conducted simulations for the COST239 and NSFNET networks in a dynamic scenario with 20-Erlang traffic load.Figure 8(a)shows the results for the COST239 network.We can see that SAT can outperform SAP and SATP in VEON blocking probability at the cost of much more traffic lost in VEONs.This is because,as aforementioned,SAT discards all traffic demands after spectrum trading and more network resources are available for establishing future new VEONs.Although both allow spectrum purchasing,SATP can always outperform SAP because of spectrum trading.Moreover,with an increasing satisfaction ratio,the VEON blocking probabilities in all the three cases increase.This is because a larger satisfaction ratio corresponds to larger amounts of bandwidth required to be allocated to each VEON,leading to a higher blocking probability.However,the traffic lost in VEONs shows an opposite trend to the VEON blocking probability.This is because a larger satisfaction ratio in the SA stage means that the VEONs are allocated more network resources initially,which gives them a higher tolerance for the traffic surge.When the satisifaction ratio reaches 0.9,even without spectrum purchasing,SAT can carry most of its traffic,while achieving a VEON blocking probability close to SAP and SATP.

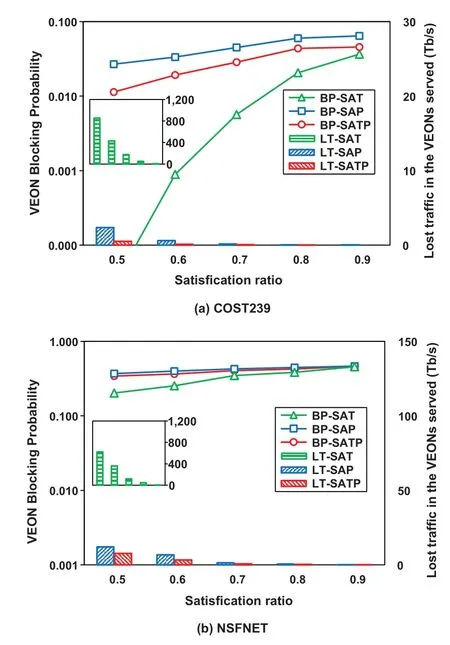
Figure 8. Impact of satisfaction ratio α on the SATP performance in the large networks.

Figure 8(b)shows the results for the NSFNET network.It is found that the performance trend here is similar to that for the COST239 network.The difference is that,in the NSFNET network,the VEON blocking probability and the lost traffic in VEONs are much larger than those in the COST239 network.Moreover,in the COST239 network,the VEON blocking probabilities between SAP and SAT and SATP show a gap when the satisfaction ratio is 0.9,while in the NSFNET network,the blocking probabilities in these three cases are very close.This is because the COST239 network has a higher nodal degree,it can serve more traffic demands through spectrum trading.In contrast,the NSFNET network has a lower nodal degree,so fewer traffic demands can be served through spectrum trading,which leads to a smaller difference between the blocking probabilities of SAP and those of SAT and SATP.

VII.CONCLUSION

In this paper,we proposed a SATP scheme to minimize the provisioning cost paid by VEON users and improve the overall spectrum utilization in a virtualized EON while providing guaranteed QoS for each VEON.We defined the SATP process as an optimization problem and developed its corresponding MILP optimization model.For large networks,we also developed efficient heuristic algorithms that have low computational complexities.To validate the efficiency of the proposed schemes,simulations were conducted based on different test conditions.Results show that compared to the benchmark,the SATP scheme can significantly reduce the cost paid by VEON users up to 14.2%,11.2%,and 11.7%for the different test networks,respectively.Moreover,the satisfaction ratio in the SA stage shows a great impact on the performance of the SATP scheme.The total cost paid by VEON clients would be large when it is too small or too large,which means that an optimal value should be identified for the best performance.Finally,we also evaluated the performance of the proposed approach in a dynamic scenario and found that the proposed scheme is efficient to reduce the VEON blocking probability and the traffic loss of VEONs significantly compared to the benchmark cases.

ACKNOWLEDGEMENT

This work was supported in part by National Key R&D Program China under Grant 2018YFB1801701,National Natural Science Foundation of China (NSFC)under Grant 61671313,and a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.