Ying-hua Xu, Wei-ping Yan, Kai-rong Qin, Tun Cao

1. School of Energy and Power Engineering, Dalian University of Technology, Dalian 116024, China

2. School of Optoelectronic Engineering and Instrumentation Science, Dalian University of Technology, Dalian 116024, China

Abstract: This paper presents a three-dimensional flow field simulation of the steady flows through diffusers and nozzles with straight or serrated-sided walls to analyze the effect of the channel structure on the flow characteristics. The pressure and velocity profiles in the diffusers and the nozzles as well as the net volumetric flow rate are determined. Our simulation demonstrates that the pressure and velocity profiles in the serrated diffuser/nozzles are more complicated than those with the straight-sided wall, while the net steady flow rate with the straight-sided wall increases monotonically with the increase of the pressure difference, the steady flow rate with serrated sided walls increases gradually to reach a maximum and then decreases with the increase of the pressure difference. The results suggest that the number of the sawteeth plays a significant role in optimizing the design of serrated diffusers and nozzles for improving the transport efficiency of valveless micro-pumps.

Key words: Valveless micro-pump, steady flow, diffuser and nozzle, serrated-sided wall, three-dimensional flow field simulation

Introduction

The microfluidic drives are important parts in the microfluidics, and the micropumps are central components of a large variety of microfluidic applications and devices such as the micro fuel cells[1], the trace drug dispensing and injection systems[2], the liquid cooling systems[3-4], the micro satellite propulsion systems[5], and the biochemical analysis[6]. The micropumps can be categorized by the design of their micro-structures. Some design items include the diffuser/nozzle micro channels[7-9], the straight sided pipes[10], the flap valves[11], the two-stage pump designs[12], the multi-chamber phase change designs,the magnetic pole channel and the electrode microchannel in the magnetohydrodynamics (MHD)[13]and the electrohydrodynamics(EHD)[14]micropumps. The valveless micropumps draw a considerable attention with their great reliability, long operating life, and because they do not plug up easily. In a diffuser/nozzle valveless micropump, the microvalve is replaced with two simple wedge-shaped channels having a relatively easy fabrication[15], which can be operated with many kinds of drivers[16], and allows a precise flow control to ensure that the living cells are not damaged by the fluctuating flow. They are thus suitable for many applications in biological and chemical synthesis.

The first diffuser/nozzle valveless micro-pump was built in 2015 by Salari and Dalton[17]. As shown in Fig. 1, a diffuser/nozzle valveless micropump consists of one single chamber with a diaphragm that is lifted and pushed back at a certain frequency by an actuator, and the pump chamber is connected to a diffuser channel for the fluid intake and a nozzle channel to export the fluid. The channels are both connected at their wider end to the pump chamber, but the diffuser and the nozzle differ in their basic volumetric flow rate, greater in the diffuser than in the nozzle in both the intake and outflow phases:Qi,d＞ Qi,n, Qo,d＞ Qo,n, where Q stands for the volumetric flow rate, o for the outlet, i for the inlet,d for the diffuser, and n for the nozzle. It follows that:Qi= Qi,d-Qi,n＞0, Qo=Qo,n-Qo,d＜0. This ensures the valveless unidirectional steady flow of the pump.The direction of the flow in the diffuser is always opposite to that in the nozzle since the pump reciprocates between the intake and outflow phases.So a “diffuser” becomes a “nozzle” when the flow direction is changed, and vice versa. The fluid is sucked into the pump chamber predominantly through the diffuser when the pump's diaphragm is lifted and is expelled predominantly through the nozzle as the diaphragm is pushed down.

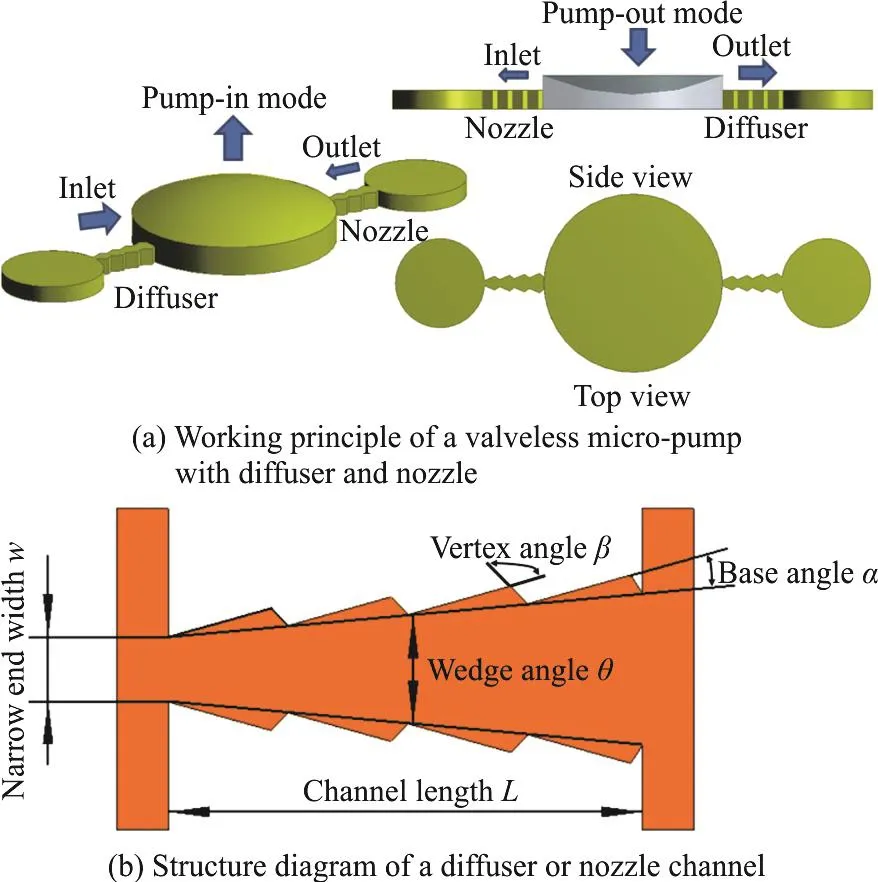
Fig. 1 (Color online) A valveless micro-pump with one single chamber and diffuser/nozzle channels

Following Sima et al.[18], a number of diffuser/nozzle valveless pumps were designed by adding more chambers to improve the pumping performance.Although adding more chambers can improve the overall efficiency of micro-pumps, the efficiency of each chamber is not improved. So the structure of the diffuser or nozzle becomes a major concern of studies.Kim et al.[19]designed the Tesla-type channel to optimize the valve body. Wang et al.[20-21]Study of the flow mechanism in the valve-less micropump may help to further improve the pumping efficiency, the high velocity fluid generates a vortex in the interfacial area of the nozzle and chamber. Such a vortex works as a “virtual valve”, which can block the reflux and result in unidirectional flow. Izzo et al.[22]optimized the diffuser and nozzle channel structures by using the whirlpool principle and proposed a diffuser and nozzle model with eddy zones. Recently, Zhu et al.[23]designed a serrated diffuser/nozzle valveless micropump with four pairs of sawteeth, each with a base angle of 10° and a vertex angle of 90°. With a computational fluid dynamics (CFD) simulation, they show that the sawtooth structures could reduce the difference between its positive and negative flow rates.Afterwards, based on the design by Guan et al.[24]modified the vertex angles from 90° to 120° and also analyzed the influence of the length, the width, the wedge angle, and the depth on the steady flow by a CFD simulation. However, the effect of the number of sawteeth on the steady flow in the serrated diffusers/nozzles was not investigated in their work. In addition,their flow field simulationswere two-dimensional.Particularly, the wall effect of any micro-channel on the viscous fluid flow cannot be ignored as the sizes of the diffusers/nozzles are decreased down to microscale. Therefore, a knowledge of the threedimensional flow field is vital for characterizing the microscale diffusers/nozzles.

This paper presents a three-dimensional simulation of the flow field through diffusers and nozzles with straight or serrated side walls of a diffuser/nozzle valveless micro-pump by using the ANSYS FLUENT 15.0 (ANSYS Inc.). We analyze the effect of the channel structure on the flow characteristics, including the pressure and velocity profiles as well as the relationship between the pressure difference and the net flow rate to provide a basis for optimizing structural parameters to improve the pumping performance.

1. Model and methods

1.1 Structure of simulation model

Fig. 2 (Color online) Structure parameters of diffuser/nozzles: Straight-sided channel (n=0) and channels with pairs of uniform sawteeth with a common base angle

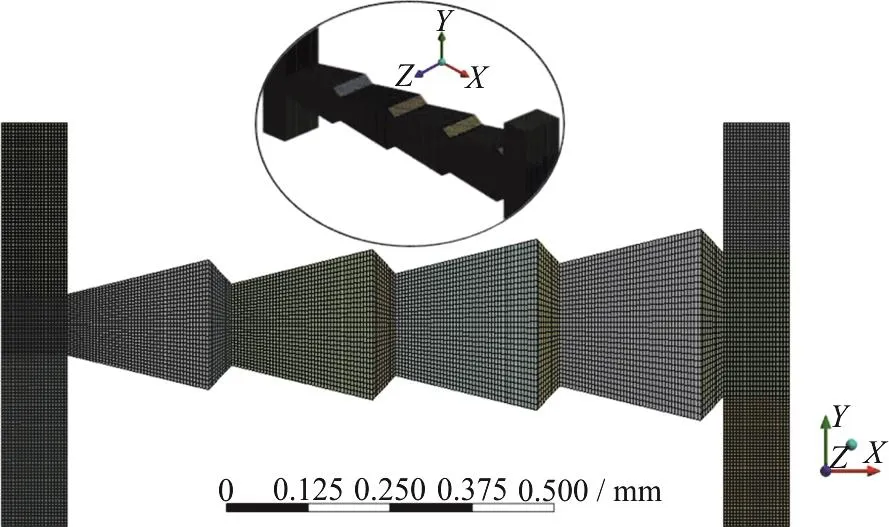
Fig. 3 (Color online) Illustration of sawtooth channel surface mesh

The proposed diffuser and nozzle channels have two different shapes: (1) simple truncated wedges with rectangular straight side walls, (2) a “uniform serrated” type with sawteethee of the same base angle α. The two types of structures are shown in Fig. 2.The longitudinal section of the type a is an isosceles trapezoid with the wedge angle θ=7°, while in the type b, the area is expanded by sawtooth triangles along both sides. The common sawtooth base angle of the uniform sawtooth channels is α=10° while the sawtooth base angles of variable channels increase from the narrow end to the wide end of the channel.To calculate the area of the longitudinal section of the serrated channels, the wedge angle θ is replaced by a virtual wedge angle Θ, between the straight lines running from points A and B at the narrow end of the channel through the respective sawtooth vertex closest to the wide channel end. The other parameters include the channel length L=1mm, the width of the narrow end w =0.09 mm , the channel depth d =0.15 mm ,the angle of the sawtooth vertex β=120°. The channel width at its wide end WTis determined by the wedge angle θ (for straight-sided channels) or the virtual wedge angle Θ. The channel types investigated in this study are thus the “straight-sided”one without sawtooth (n=0), and the “uniform serrated” one with 1-5 uniform sawteeth pairs (n=1,n =2, n=3, n=4 or n=5).

1.2 Simulation models

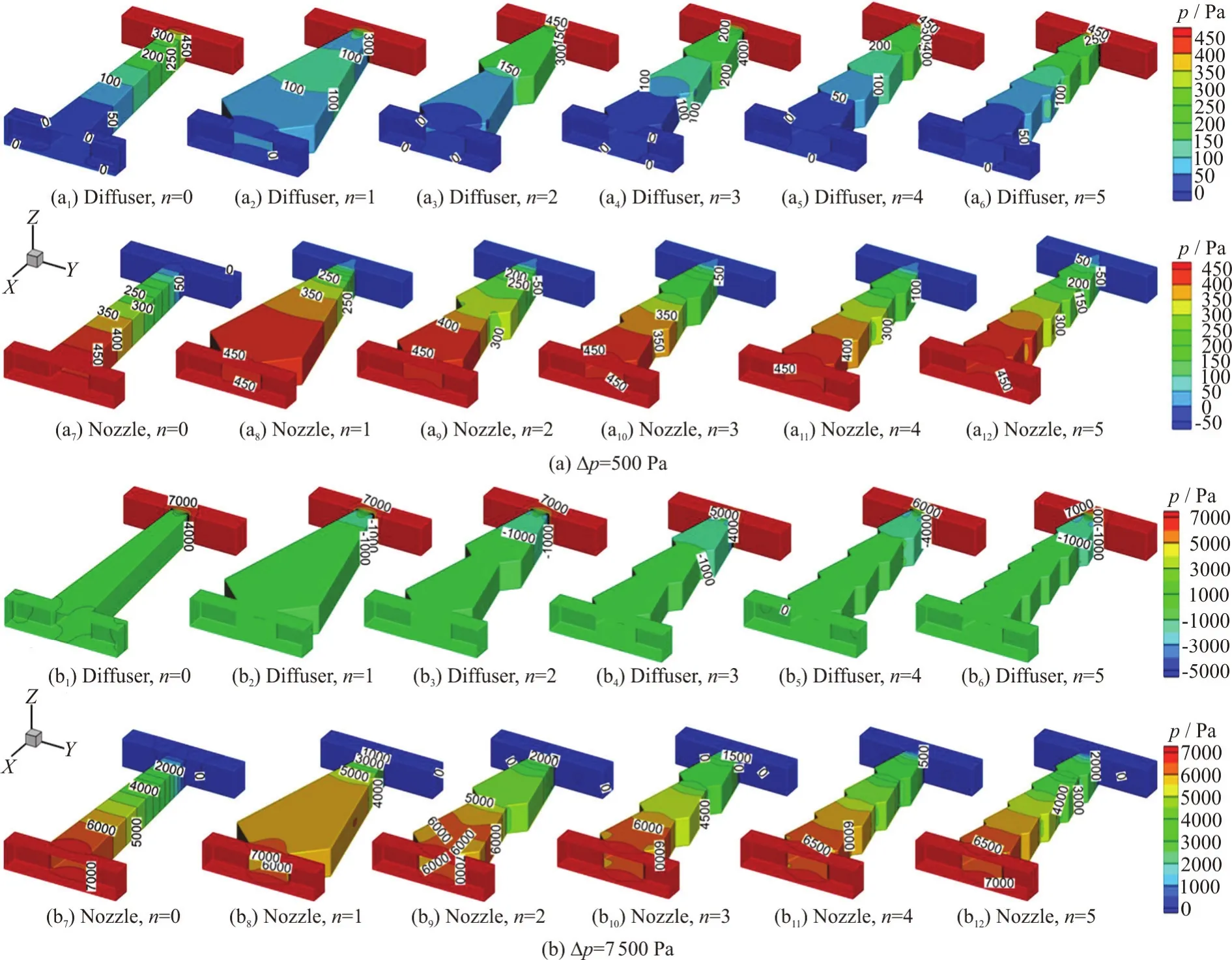
Fig. 4 (Color online) The band plot of three-dimensional pressure in the diffusers and nozzles with straight-sided walls and uniform sawteeth at Δp=500 Pa, 7 500 Pa, respectively

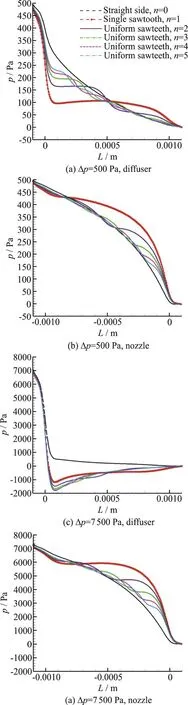
Fig. 5 (Color online) Pressures against the length x of the diffusers and nozzles with straight-sided walls and uniform sawteeth at Δp=500 Pa, 7 500 Pa

In this study, the steady flows through the diffusers/nozzles as shown in Fig. 2 are simulated by the ANSYS FLUENT15.0 (ANSYS Inc.), visualized by the Tecplot 360 2015 (TecPlot, Inc.). In all simulations, the sweep method is used to generate hexahedron mesh with the Workbench Mesh with the mesh size of 5×10-6m, which is suitable for viscous sublayers of a dimensionless distance of y+＜5 from the first layer mesh centroid to the wall. Meshrefined surfaces and an enlarged view of one mesh surface are shown in Fig. 3. To investigate the characteristics of the flow through diffusers and nozzles influenced by different numbers of sawteeth,simulations are carried out with the k-ω SST turbulence model.

Herein, the fluid density is ρ=1000 kg/m3, the dynamic viscosity of 20°C water μ= 10-3Pa? s, the length of the channel L=1mm, the height d=0.15 mm, the narrower width w=0.09 mm , and the vertex angles of the all sawteeth are identical, β=120°, the pressure psat the outlet of a diffuser/nozzle is set to be zero, i.e., ps=0 while the pressure poat the inlet is a constant in the range of 100 Pa-10 000 Pa, Δp is defined as Δp = po- ps.

The pressure and velocity profiles along the diffusers/nozzles could be directly obtained from the FLUENT software. Once the velocity profiles are obtained, the steady volumetric flow rates through the diffusers or nozzles could be calculated by the integration over the cross-section. The net volumetric flow rate is calculated by the difference between the flow rate through the diffuser and that through the nozzle. The pressure loss coefficient ξ is calculated by the following equation

where p, v are the pressure and the sectionaveraging velocity along the length of the diffuser/nozzle channel, respectively.

2. Results and discussions

2.1 Pressure distribution in the diffusers/nozzles with straight-sided walls and uniform sawteeth

The band plot of the three-dimensional pressure in the diffusers and nozzles with straight-sided walls and uniform sawteeth at Δp=500 Pa, 7 500 Pa are shown in Figs. 4(a), 4 (b), respectively.

It can be seen from Fig. 4 that the pressure drop in a diffuser is greater than that in a nozzle since the pressures at the entrance of the diffuser and the nozzle remains the same, and the widening diffuser decreases the pressure rapidly.

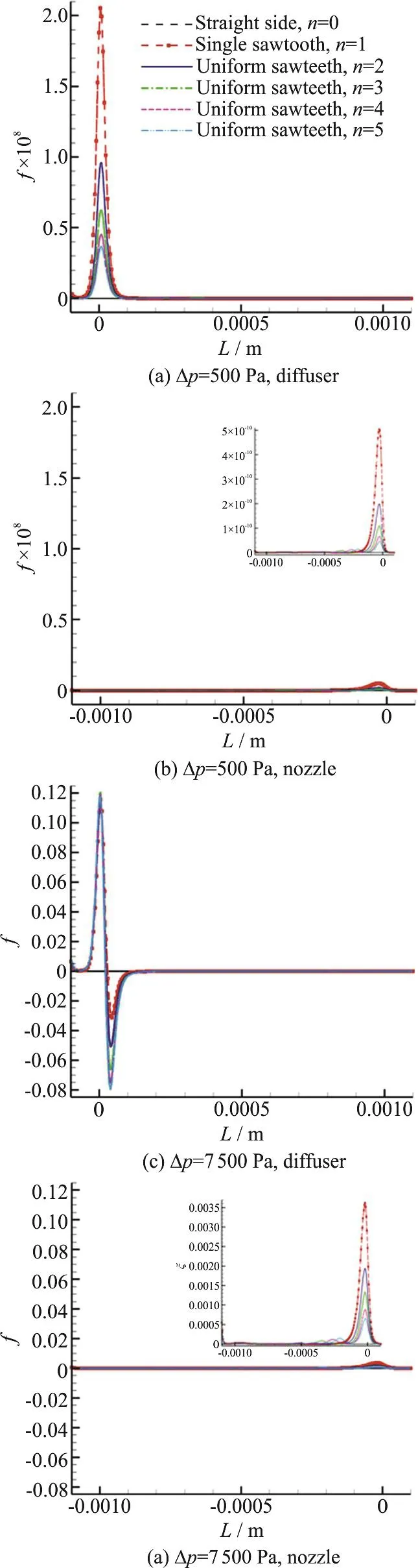
Fig. 6 (Color online) Pressure loss coefficients against the length x of the diffusers and nozzles with straight-sided walls and uniform sawteeth at Δp=500 Pa, 7 500 Pa

To clarify this point, the pressures against the length x of the diffusers and the nozzles at Δp=500 Pa-7 500 Pa, are compared in Fig. 5. It is worth noting that the pressure in the straight-sided diffuser or nozzle decreases monotonically while those in the serrated diffusers or nozzles decrease in an oscillating way (Fig. 5). It is also seen from Fig. 5 that the number of the oscillations is the same as the sawtooth number, and the oscillating amplitude deceases with the increase of the number of the sawteeth.

2.2 Pressure loss coefficient along the length of the diffusers/nozzles with straight-sided walls and uniform sawteeth

Figure 6 shows the pressure loss coefficients along the length of the diffusers/nozzles with straight-sided walls and uniform sawteeth at Δp=500 Pa, 7 500 Pa. It is observed from Fig. 6, where f is the pressure loss coefficient. While the pressure loss coefficient is close to zero along the length of the diffuser/nozzle with straight-sided walls, those for the diffusers/nozzles with uniform sawteeth are not zero along the full length; this pressure loss coefficient is related with the number of sawteeth, it is worth pointing out that the pressure loss coefficients in the diffusers are larger than those in the nozzles, which ensures that the volumetric flow rates through the diffusers are larger than those in the nozzles.

2.3 Flow velocity distribution in the diffusers/nozzles

with straight-sided walls and uniform sawteeth

Figures 7(a), 7(b) show the three-dimentional distributions of the velocity in the x-direction in the diffusers and nozzles with straight-sided walls and uniform sawteeth at Δp=500 Pa, 7 500 Pa, respectively. From Figs. 7(a), 7(b) it is observed that the steady flow in the diffuser or nozzle with straightsided walls is laminar at Δp=500 Pa or 7 500 Pa.However, the steady flow in the serrated diffusers or nozzles is turbulent at Δp=7 500 Pa while it is laminar at Δp=500 Pa. Eddies or vortices could be found around the corners of the serrated walls. These eddies or vortices become larger by decreasing the number of sawteeth.

Figure 8 shows the velocity profiles in x-direction against the width of the outlet at the plane z=d /2 in the diffusers and nozzles with straight-sided walls and uniform sawteeth at Δp=500 Pa, 7 500 Pa,respectively, where W is the width of the outlet, Vxis the velocity profile in x-direction. It can be clearly seen from Fig. 8 that the maximum velocities in x-direction at the outlets of nozzles are always larger than those at the outlets of diffusers. However,the volumetric flow rate through a nozzle is always smaller than that through a diffuser because the area of the cross section of a nozzle is much smaller than that of a diffuser.

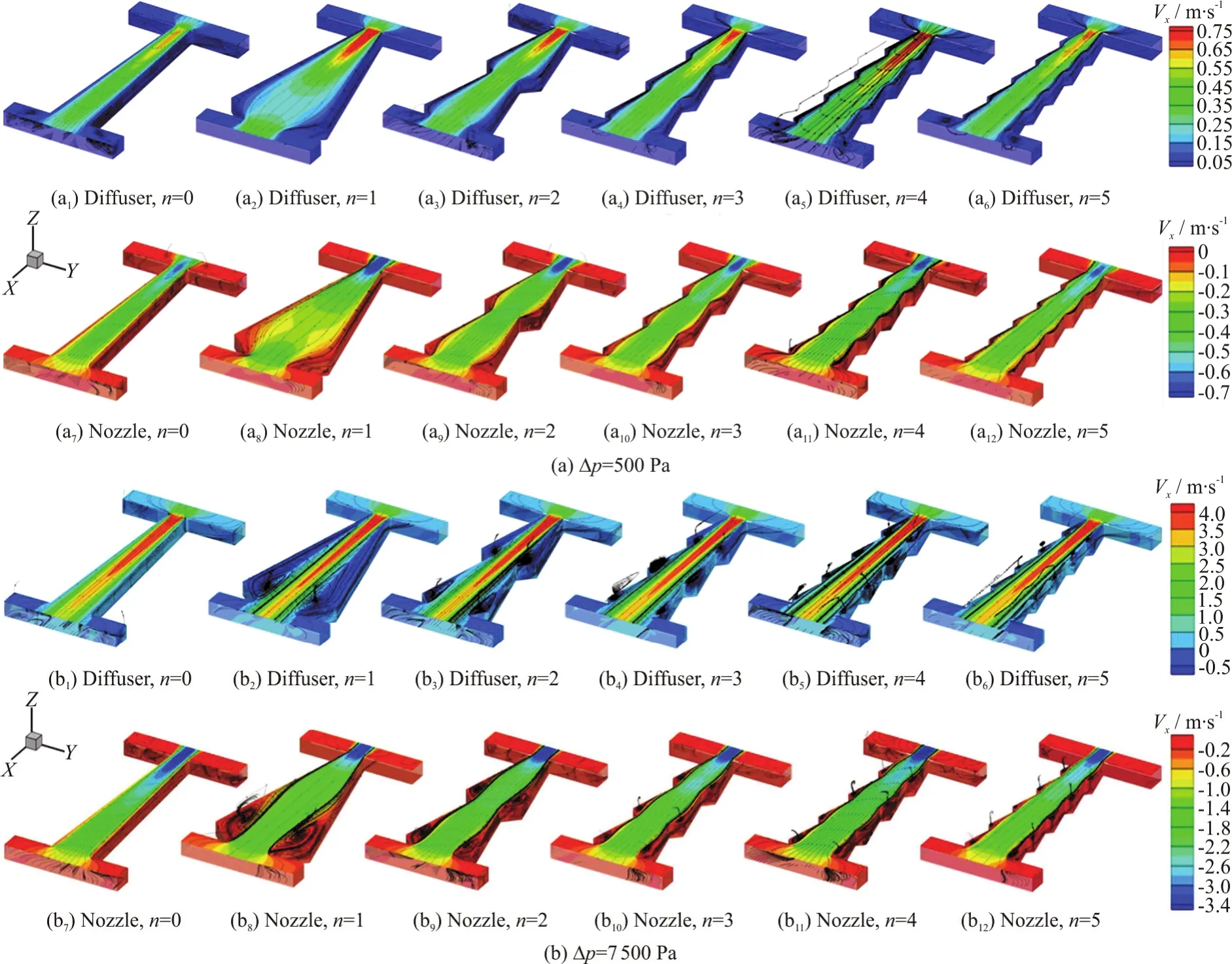
Fig. 7 (Color online) Distributions of flow velocity in x-direction in the diffusers and nozzles with straight-sided walls and uniform sawteeth at Δp=500 Pa, 7 500 Pa, respectively

At a low pressure difference Δp=500 Pa , the maximums of the velocities in x-direction at the outlet of the diffusers or nozzles decrease with the increase of the number of sawteeth, however, at a high pressure difference Δp=7 500 Pa, the velocities in x-direction at the outlet of the diffusers/nozzles may increase or decrease with the increase of the number of sawteeth, which demonstrates that the number of sawteeth plays an important role in regulating the outlet flow rate of the diffuser/nozzle.

2.4 Relationship between pressure difference and net steady volumetric flow rate in the diffusers/nozzles with straight-sided walls and uniform sawteeth

In order to understand the pumping performance for different kinds of diffuser/nozzle valveless micropumps, the relationship between the pressure difference and the net steady volumetric flow rate corresponding to different diffusers/nozzles with straight-sided walls and uniform sawteeth are shown in Fig. 9, where Dpis the pressure difference, Q is the net steady flow rate in the diffusers/ nozzles. It is shown that for the diffuser/nozzle with straightsided walls, the net flow rate increases monotonically with the increase of the pressure difference; but for the diffusers/nozzles with uniform sawteeth, the net flow rate increases gradually to the peak and then decreases gradually when the pressure difference increases. It is worth noting that for the diffusers/nozzles with uniform sawteeth, the flow rate increases with the increase of the number of sawteeth before any flow rate reaches its maximum (i.e., when the pressure difference is low), however, the flow rate decreases with the increase of the number of sawteeth after the flow rate reaches its maximum (i.e., when the pressure difference is high). In addition, the relationship between the pressure difference and the net flow rate is related with the number of the sawteeth.

3. Conclusion

In order to analyze the effect of the channel structure on the flow characteristics, we carry out athree-dimensional flow field simulation of the steady flows through diffusers and nozzles with straight or serrated-sided walls. The simulation results demonstrate that the steady flow in the diffuser/nozzle with straight-sided walls is laminar but that in the serrated diffuser/nozzles is a disturbed flow. The net steady flow rate through the diffusers and nozzles with straight-sided walls increases monotonically as the pressure difference rises, however, the steady flow rate through the diffusers and nozzles with serrated sided walls increases gradually to reach the peak and then decreases with the increase of the pressure difference. This relationship between the pressure difference and the net flow rate is related with the number of the sawteeth. The results suggest that the number of the sawteeth is a critical factor in optimizing the design of serrated diffusers and nozzles of valveless micro-pumps.

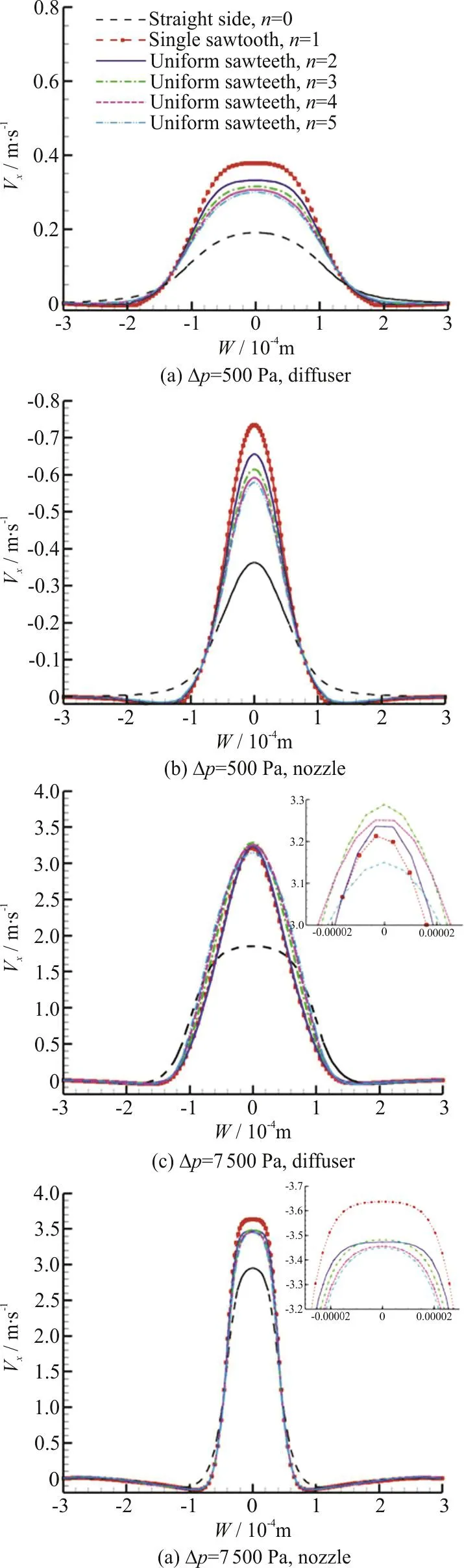
Fig. 8 (Color online) The velocity profiles in x-direction against the widths of the outlet at the plane z=d/2 in the diffusers and nozzles with straight-sided walls and uniform sawteeth at Δp=500 Pa, 7 500 Pa, respectively

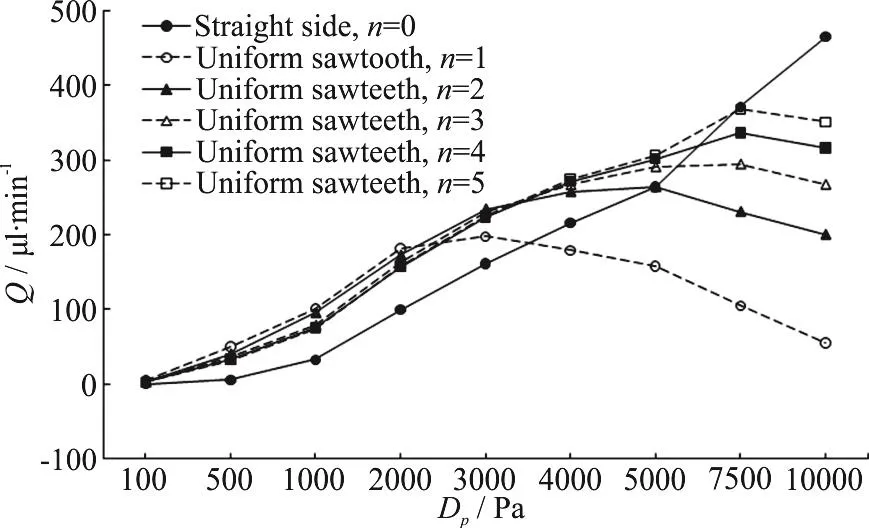
Fig. 9 Relationship between pressure difference and net steady flow rate in the diffusers/nozzles with straight-sided walls and uniform sawteeth