Muhammad Ijaz Khan, Tasawar Hayat, , Muhammad Waqas, Ahmed Alsaedi, Muhammad Imran Khan

1. Department of Mathematics, Quaid-I-Azam University, Islamabad, Pakistan

2. Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah, Saudi Arabia

3. Heriot Watt University, Edinburgh Campus, Edinburgh, UK

Abstract: Our interest here in this investigation is to explore the thermophoresis and Brownian motion characteristics in flow induced by stretched surface. Electrically conducted Jeffrey material formulates the flow equation. Linear forms of stretching and free stream velocities are imposed. Nonlinear radiation and convective heating processes describe the phenomenon of heat transfer.Passive controls of nanoparticles are considered on the boundary. The compatible transformations produce the strong nonlinear differential systems. The problems are computed analytically utilizing HAM. Convergence domain is determined and major results are concluded for different parameters involved. Heat transfer rate and drag force are also explained for various physical variables.Our analysis reveals that heat transfer rate augments via larger radiation parameter and Biot number. Moreover larger Brownian motion and thermophoresis parameters have opposite characteristics on concentration field.

Key words: Jeffrey nanomaterial, non-linear radiative heat flux, convective boundary conditions, Brownian and thermophoresis diffusions

Introduction

Fluid material consisting of nanometer sized elements is identified as nanofluid. Inclusion of nanoparticles develops thermal features of base liquid.Existing literature on nanofluids determines that the properties of the liquid are distinct through the combination of nanoparticles. No doubt the base liquids have lower thermal conductivity than these particles. Nanoliquids have ample demands in medical,electrical and engineering subjects. Cooling and heating frameworks in industries, hyperthermia,electronic devices batteries and modern drug delivery systems are some common demands of nanoliquids.Numerous investigations regarding nanofluids under distinct flow configurations have been reported after the revolutionary work presented by Choi and Eastman[1]. For illustration Ramesh and Gireesha[2]investigated the features of heat sink/source and convective heating condition in stretchable flow of Maxwell nanomaterial. Melting heat and chemical reaction aspects in stretchable flow of Williamson nanomaterial filling the permeable space is scrutinized by Krishnamurthy et al.[3]. Turkyilmazoglu[4]scrutinized the magnetohydrodynamic slipped flow of nanoliquids. Radiative and convective conditions characteristics in stagnation point flow of Maxwell nano-liquid are disclosed by Hayat et al.[5].

Radiation effect has many applications in physics,engineering and industry including polymer processing, glass production, nuclear reactors and in space technology like in power plants, rocket and missiles.Sunlight, also called solar radiation is a form of radiation that originated from the Sun. The particular components of sun/solar energy are that it never runs out, no burning or motion are required in the energy-change process, there is no clamor, and there are different energy capacities. Jeffrey liquid flow with heat generation/absorption and thermal radiation over a semi-infinite vertical plate is analyzed by Gaffar et al.[6]. Stagnation point flow of Oldroyd-B liquid with nonlinear thermal radiation is discussed by Hayat et al.[7]. MHD nanoliquid flow with entropy generation and nonlinear radiation in a porous vertical microchannel is examined by Lopez et al.[8]. Marangoni boundary layer flow of nanofluid with thermal radiation driven by an exponential temperature is studied by Lin et al.[9]. Chemically reactive flow of tangent hyperbolic nanomaterial with double diffusive convection and thermal radiation is reported by Hayat et al.[10].

These days several investigators in engineering and scientific areas have shown huge interest in non-Newtonian materials since these materials play a crucial part in industrial developments. Muds, soaps,emulsion, apple sauce, chyme, shampoos etc. are daily life examples of non-Newtonian materials. The non-Newtonian materials in general are classified into differential, rate and integral types. Available literature does not offer any real solitary relation that entirely describes the individual features of nonviscous materials. Jeffrey fluid model belongs to the class of rate type fluids which can predict the characteristics of retardation and relaxation time.Turkyilmazoglu and Pop[11]calculated exact analytical solutions of Jeffrey material in the region of a stagnation point flow. Hayat et al.[12]worked on chemically reactive flow of Jeffrey liquid with Newtonian and Joule heating effects. Analysis of Jeffrey liquid flow inside oscillating rotating disks is discussed by Reddy et al.[13].

Flow characteristics in the neighborhood of stagnation point are still a topic of hot interest for the recent scientists and researchers. Such interest is mainly due to its prominent demands in industrial and engineering process. Stagnation point has significant role in flow of ground water since the several streamlines advancing through them portray diverse flow regions. Melting heat transfer effect in stagnation point flow of water-carbon nano-liquid is examined by Hayat et al.[14]. Further Hayat et al.[15]considered non-Fourier heat flux in a stagnation point flow with isothermal chemical reaction. Soid et al.[16]worked on stagnation flow of axisymmetric viscous liquid considering second order velocity slip. Effect of non-Fourier heat flux with temperature dependent thermal conductivity over a stretched surface is discussed by Hayat et al.[17].

Although the above investigation examined the stagnation point flow of Jeffrey nanomaterial bounded by a stretched surface. Only few articles in literature systematically described the stagnation point flow of Jeffrey nanomaterial over a stretched surface and to the best of our knowledge, no research has been carried out on the existence of non-linear radiation and convective boundary condition involving Jeffrey nanomaterial. Therefore, this was the motivation of the present flow problem. The problem is first modeled and then solved by HAM[18]. Series solutions of derived flow problem are obtained. Behavior of different variables on the flow and heat and mass transfer characteristics are examined and discussed.

1. Formulation

We consider the steady MHD two-dimensional flow of Jeffrey nanomaterial over a stretched surface positioned at y=0. Non-linear thermal radiation and stagnation point flow aspects are also taken into consideration. Flow is conducting electrically with constant applied magnetic field. Linear forms of stretching and free stream velocities with constant surface thickness are imposed. Under these conditions the boundary layer equations are[6]:

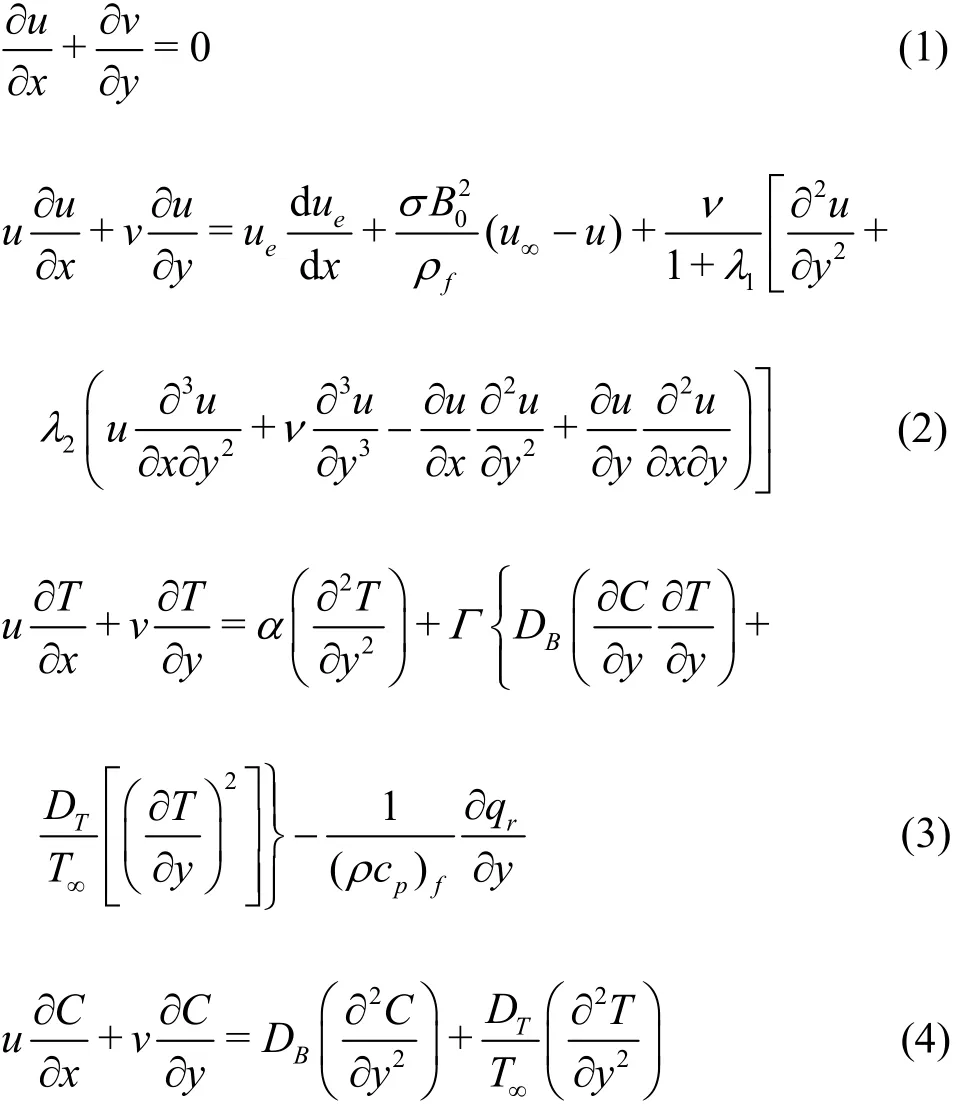
with

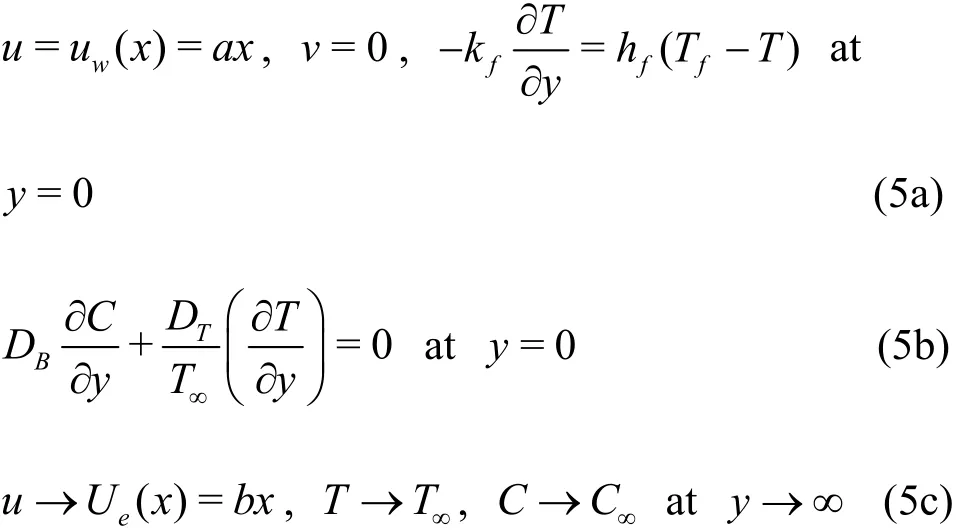
The Roseland approximation for radiation is

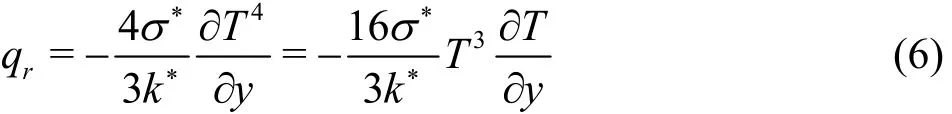
here u, v represents the velocity components, x,y the Cartesian coordinates, uethe stretching velocity, u∞the free stream velocity, σ the electrical conductivity, B0the magnetic field strength,fρ the density,1λ the ratio of relaxation and retardation times,2λ retardation time, ν the kinematic viscosity, T the temperature, α the thermal diffusivity, qrthe radiative flux, Γ the effective heat capacity of nanoparticles, DBthe Brownian diffusion, DTthe thermophoresis variable, C the concentration, T∞the ambient temperature, C∞the ambient concentration, a, b dimensional constant with represent the stretching rate, kf, hf, Tfrespectively represents the thermal conductivity, heat transfer rate and convective fluid temperature, σ*the Stefan Boltzmann constant and k*the mean absorption coefficient. Utilizing Eq. (6) in Eq. (3) we obtain the energy expression in following form

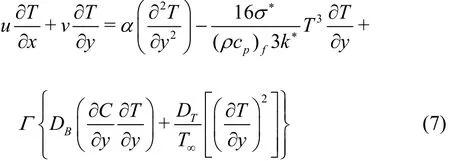
Characterize the non-dimensional temperature θ (η)=(T - T∞)(Tf-T∞) with T = T∞[1+(N r - 1)θ] and Nr = Tf/T∞.

Applying

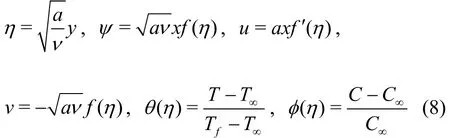
Equation (1) is identically satisfied and Eqs. (2),(4) and (7) takes the form

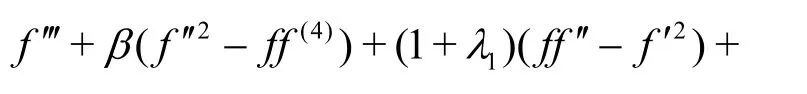
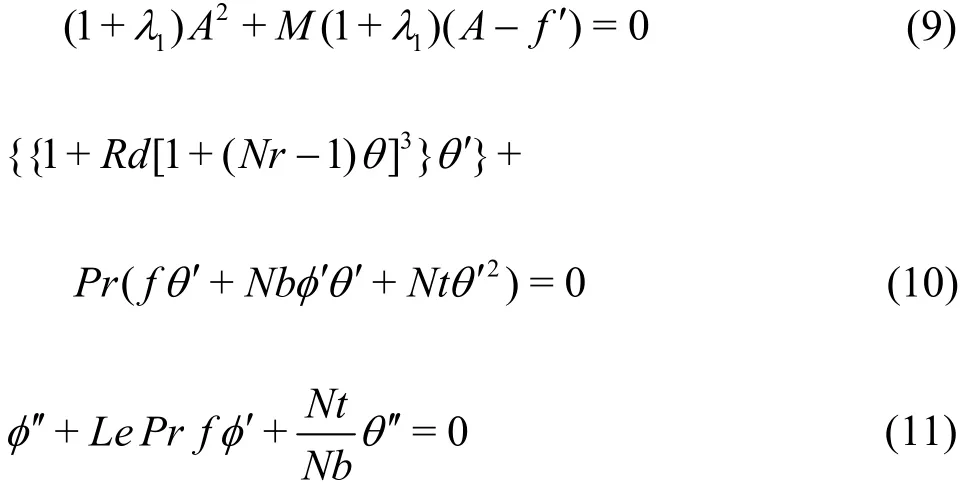
with

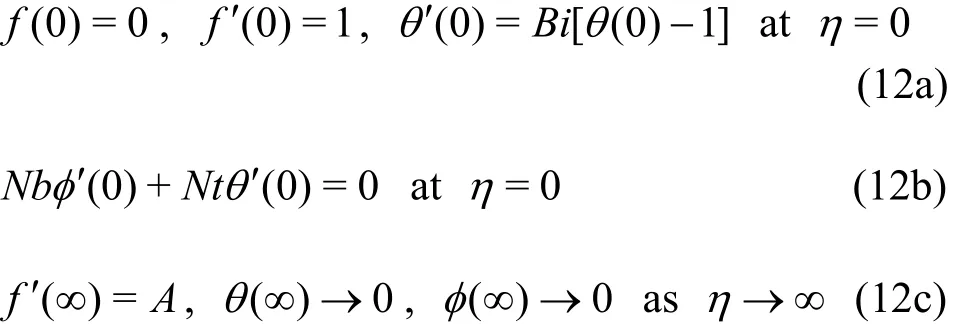
In the above expressions β the Deborah number,M the magnetic variable, A the ratio of velocities or ratio parameter, Rdthe radiation parameter, Nr the temperature ratio variable, Pr the Prandtl number, Nbthe Brownian diffusion variable, Nt the thermophoresis variable, Le the Lewis number and Bi the Biot number, These variables are mathematically defined by:

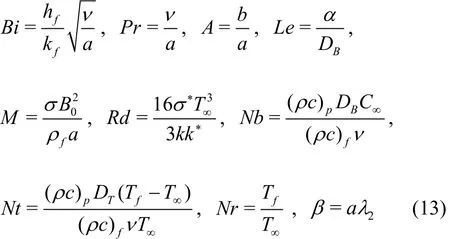
Mathematical expression for Cfx, Nuxare

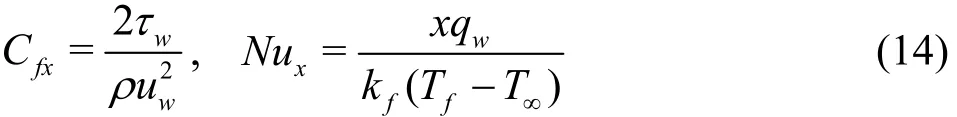
wherewτ, qware defined as

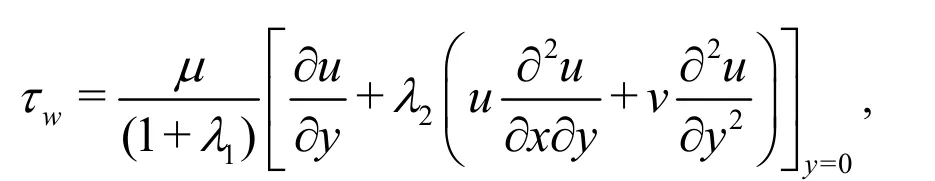
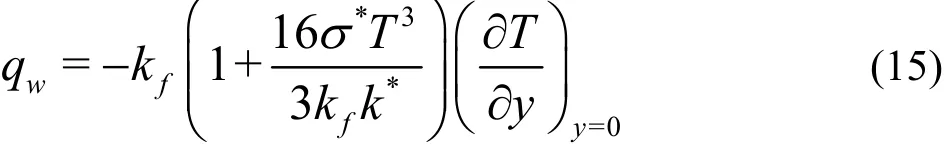
Then the final forms of these quantities are:

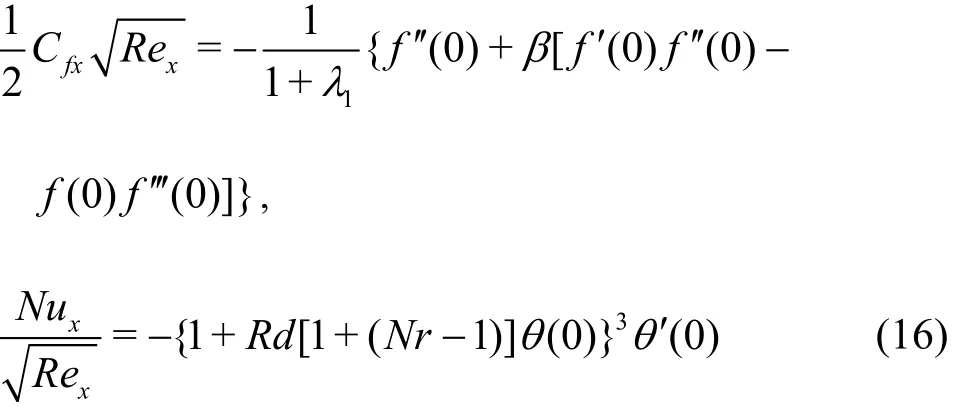
in which Rex= ax2/ν represents Reynolds number,τwthe shear stress, qwthe wall heat flux, Cfxthe local skin friction and Nuxlocal Nusselt number.

2. Series solution and analysis of convergence

The HAM was initially conceived in 1992 by Liao[18]and further modified in 1997 to present a non-zero auxiliary parameter, to develop a convergence of series solution in general form. The convergence-control parameter is a non-physical variable that gives a straightforward approach to check and authorize the convergence of solution series. The ability of the HAM is to normally show convergence of the series solution corresponding to strong nonlinear systems. For this purpose the initial approximation and operators are given below:

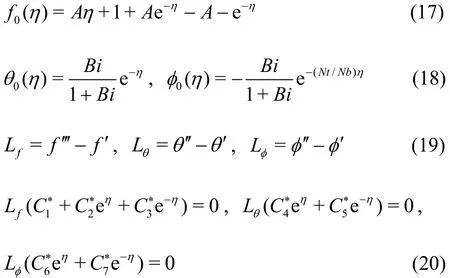
To decide the proper values of hf, hφand hφwe have organize the h-curves in Figs. 1, 2.Permissible values for interval of convergence include-1 .3 ≤ hf≤-0 .2, -1 .8 ≤ hθ≤-0 .2 and - 1.8 ≤hφ≤-0 .45.

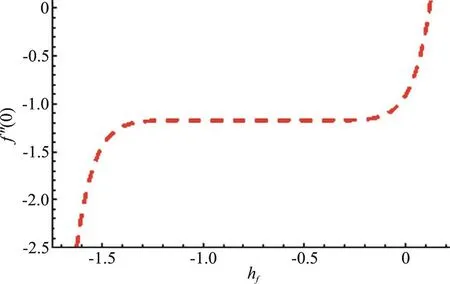
Fig. 1 (Color online) h-curve for f

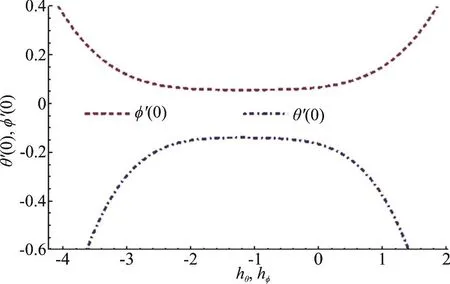
Fig. 2 (Color online) h-curve for θ, φ

The series solutions convergence is given in Table 1

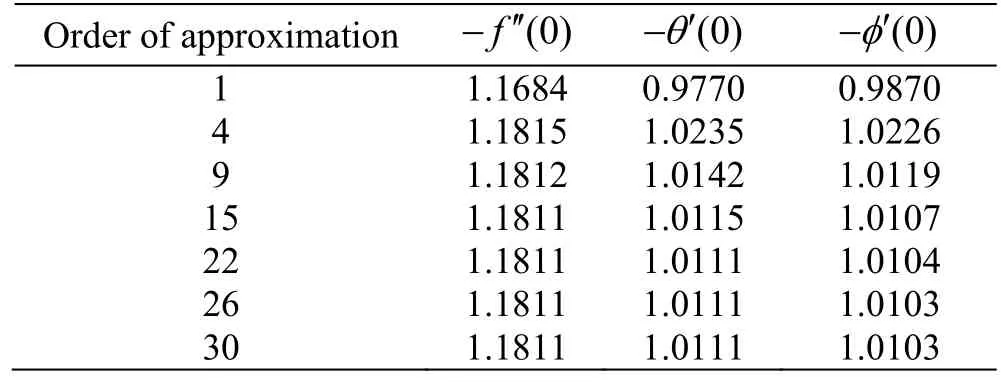
Table 1 Series solutions convergen ce w hen β = M = Le=0.1,Nt = A =λ2=0.2,Nb = Bi = Rd =0.5,Nr =0.7 and Pr=1.4

3. Discussion

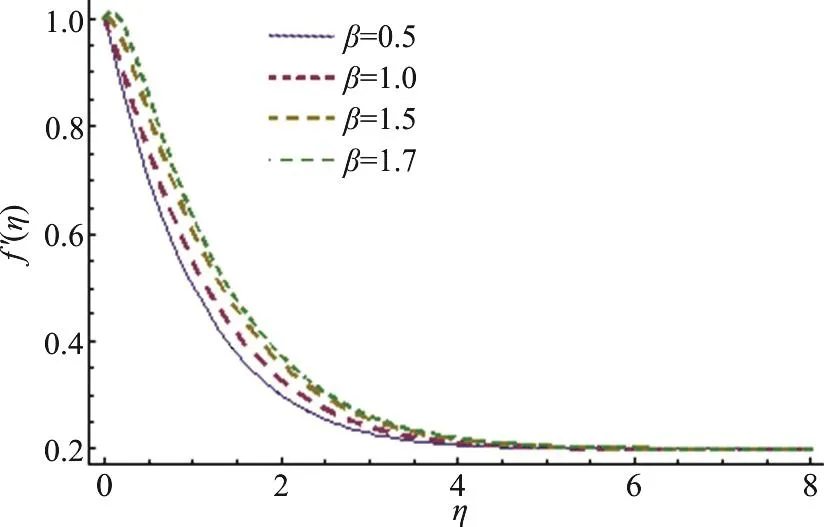
Fig. 3 (Color online) β variation for f

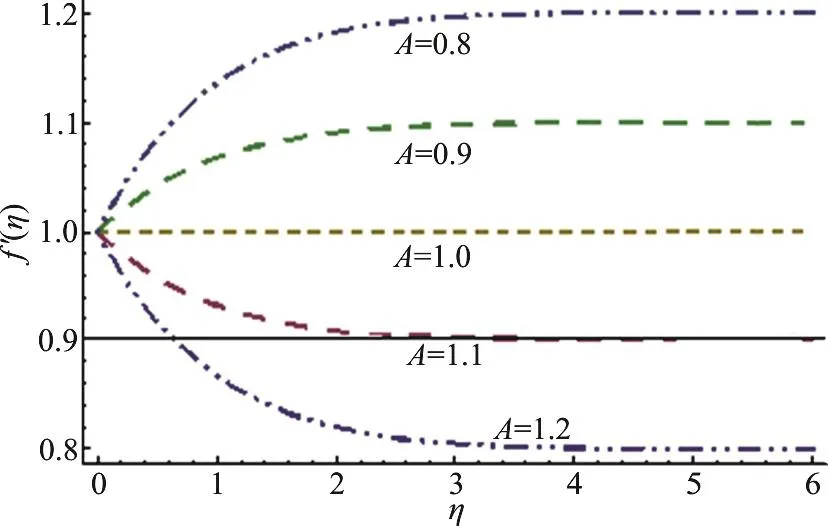
Fig. 4 (Color online) A variation for f

Fig. 5 (Color online) M variation for f

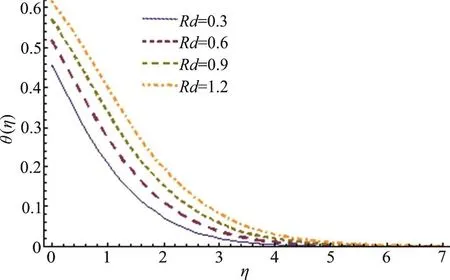
Fig. 6 (Color online) Rd variation for θ

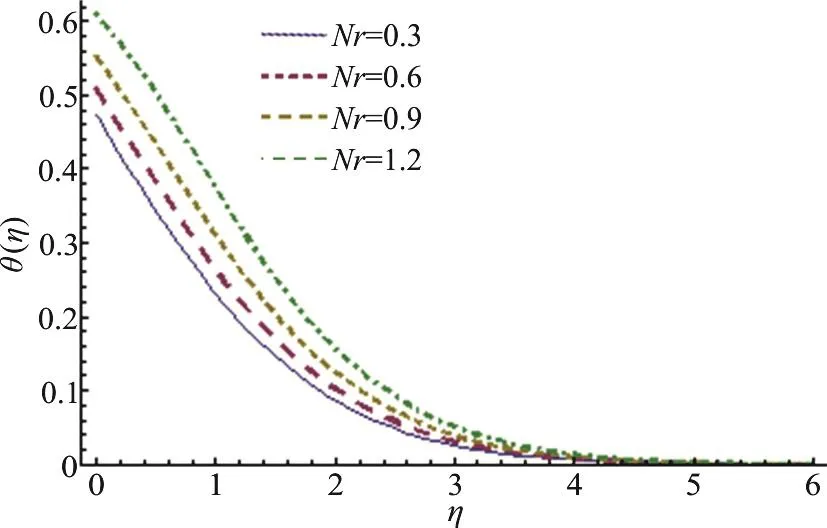
Fig. 7 (Color online) Nr variation for θ

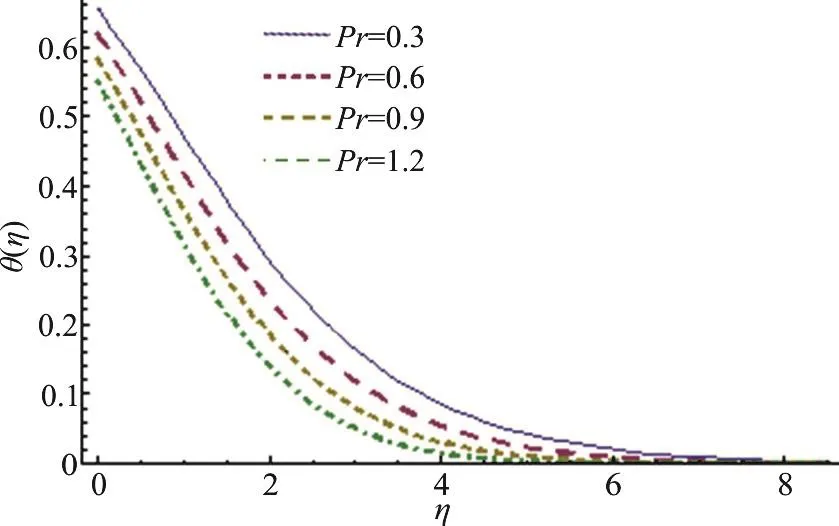
Fig. 8 (Color online) Pr variation for θ

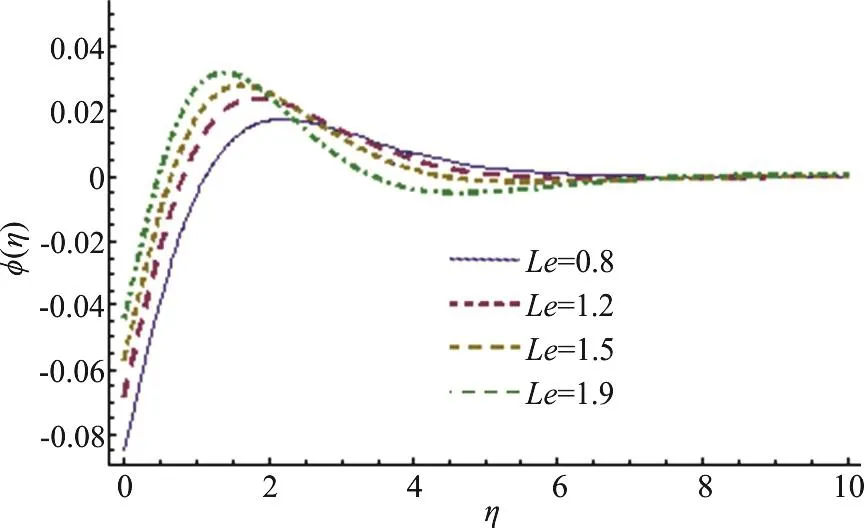
Fig. 9 (Color online) Le variation for φ

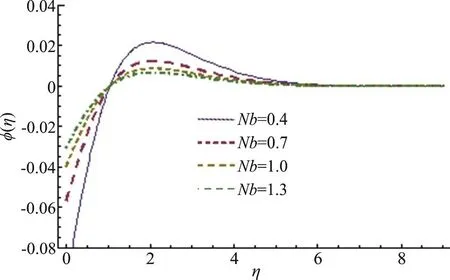
Fig. 10 (Color online) Nb variation for φ

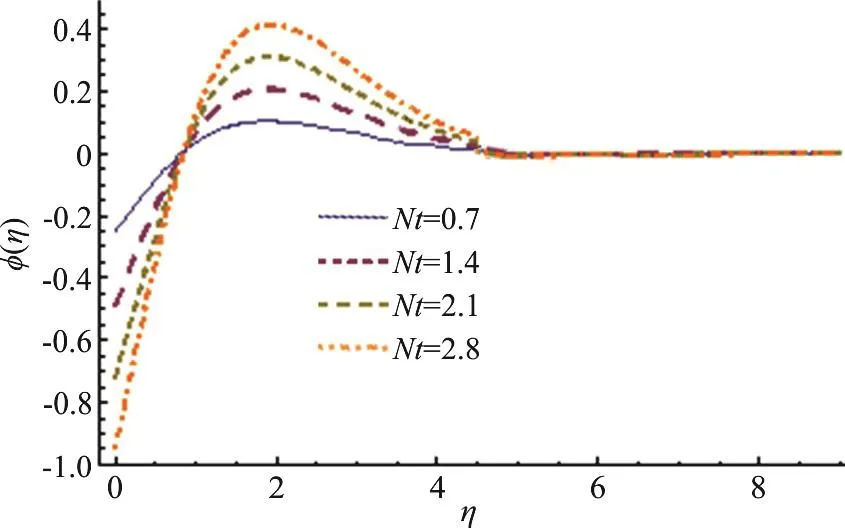
Fig. 11 (Color online) Nt variation for φ

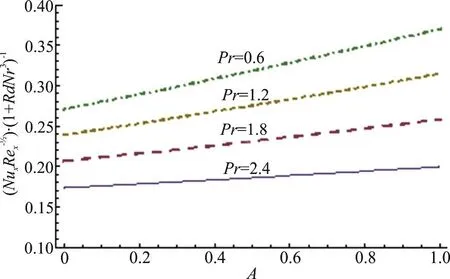
Fig. 12 (Color online) Effects of Pr, A on Nusselt number

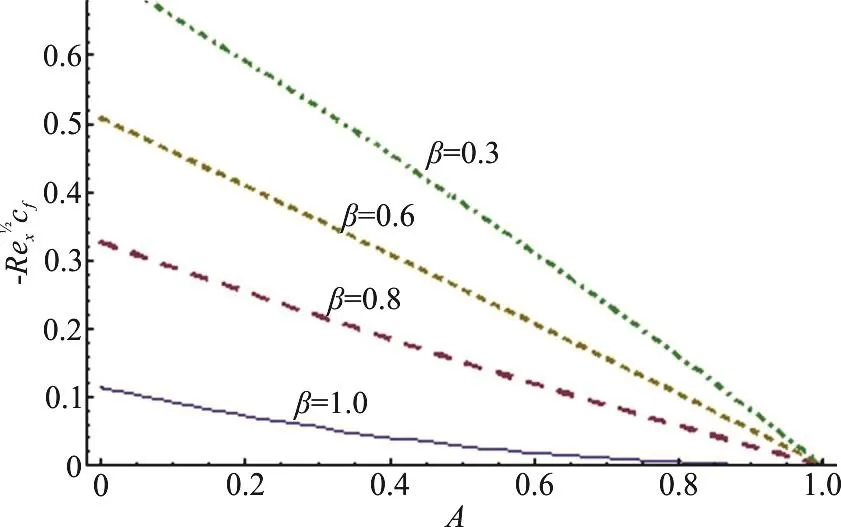
Fig. 13 (Color online) Effects of β, A on skin firction

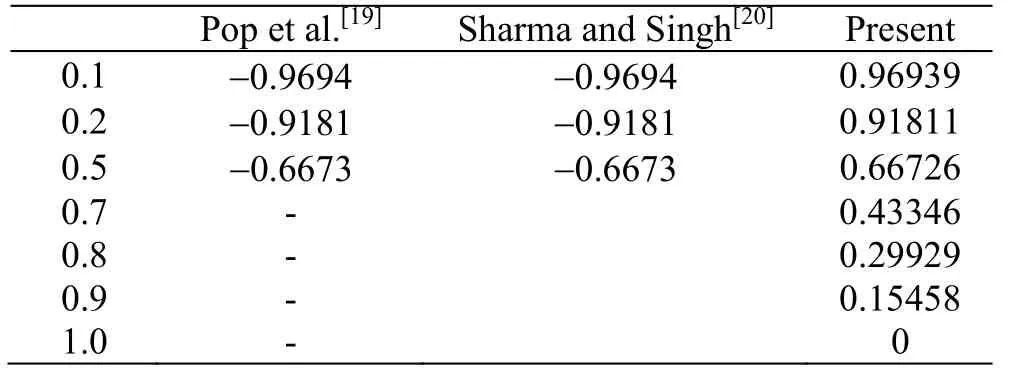
Table 2 Comparison with Pop et al.[19], Sharma and Singh[20]of A when β= M= λ2=0

This section highlights the impacts of distinct variables on velocity (f ′(η)) temperature (θ (η)),concentration (φ (η)), drag forceand heat transfer rate. Behavior of β on(f ′(η)) is presented in Fig. 3. It is noted that velocity field shows decreasing behavior corresponding to higher estimation of β. Actually β is the quantitative relation of relaxation to observation times. With anincreasein β therelaxationtime rises and generates more resistance to the fluid flow due to which (f ′(η)) decays. Figure 4 is sketched to see the behavior of A on (f ′(η)). Here velocity of fluid particle increases for higher estimation of A.For A＜1 the velocity of the fluid particles is less than the stretching velocity of the sheet. For A=1 no boundary layer formation exists, because fluid particle and sheet have the same velocity. Impact of M on velocity is sketched in Fig. 5. The comparison with pop et al.[19], Sharma and Singh[20]of A in Table 2. It is revealed from this Figure that rising values of M decelerate the fluid velocity. It leads to thinner momentum layer in the flow domain. Here intensification in Lorentz force yields more resistance to the liquid motion due to which (f ′(η)) decays.Figure 6 is plotted to show the behavior of radiation parameter (Rd) on temperature field. Temperature field enhances for higher estimation of radiation parameter. Physically more heat is produced when radiation is incremented. Therefore temperature field increases. Figure 7 is focused to describe the behavior of temperature ratio parameter (Nr) on temperature field. Both temperature and thermal layer are enhanced for higher estimation of Nr. It is due to the fact that when we enhance Nr then Tfincreases due to which more heat is transferred to the fluid and so temperature profile enhances. Figure 8 demonstrates the effect of Pr on temperature. Both (θ (η))its thermal layer decay for (0.3, 0.6, 0.9, 1.2). Since Pr depends on viscosity, thermal conductivity and specific heat. Therefore Pr is the combination of kinematic viscosity to thermal diffusivity. Larger Pr yields lower thermal diffusivity that results in reduction of temperature. Figure 9 disclosed the characteristics of Lewis number on φ. Concentration field decays for higher Le. It is due to the fact that rate of Brownian diffusion decreases for higher estimation of Le and therefore concentration field decreases. Figures 10, 11 depict the effects of Nb,Nt on concentration field. It is observed that concentration field increases for larger Nb and it decreases for higher estimation of Nt. In nanomaterial flow, due to existence of nanoparticles in the nanomaterial system the Brownian motion factor transpires and higher Brownian motion variable Nb corresponds to lower nanoparticles concentration field.Moreover the thermophoretic force rises with an increment in Nt which contributes to transfer nanoparticles from hotter to colder regions and thus increases the magnitude of nanoparticle volume fraction profile. Ultimate, the concentration layer thickness corresponds to be considerably large for marginally enhanced value of thermophoretic parameter. Figures 12, 13 indicate Nusselt number and skin friction coefficient against A, β and Pr.Here Nusselt number and skin friction are enhance for higher estimation of β, A and Pr. Physically higher Prandtl number possess a large heat capacity and hence heat phenomenon enhances.

4. Conclusions

The investigated flow problem has the following remarks:

(1) Concentration field decays for higher estimation of Nb while it enhances for larger Nt.

(2) Concentration profile decreases when Le is enhanced.

(3) Larger Bi magnifies the temperature and corresponding layer thickness.

(4) Higher estimation of M, A enhances the intensity of drag force.

(5) Influences of Biot number and thermophoresis parameter on concentration field are qualitatively similar.

Acknowledgement

The authors are grateful to the reviewers for their comments which have served to improve the present work.