吳曉明

(福建省莆田第一中學(xué))

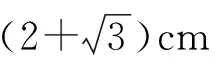
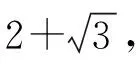
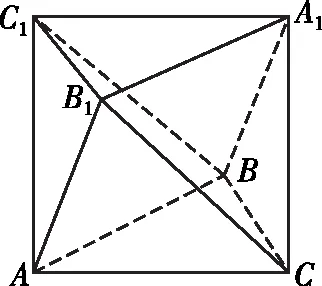
圖1

下面通過四個(gè)方法來解答.

解法一:設(shè)△ABC,△A1B1C1的中心分別為O,O1,取BC,B1C1的中點(diǎn)D,D1,過點(diǎn)D1作D1E⊥AD交AD于點(diǎn)E,如圖2.∵OO1⊥平面ABC,∴OO1⊥AD,∴四邊形EOO1D1為矩形,∴ED1=OO1,

圖2

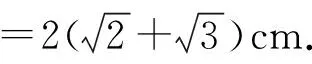
解法二:將該正八面體放置于正方體PQRS-P1Q1R1S1內(nèi),使得正八面體ABC-A1B1C1的每個(gè)頂點(diǎn)為正方體每個(gè)表面的中心,如圖3,

圖3

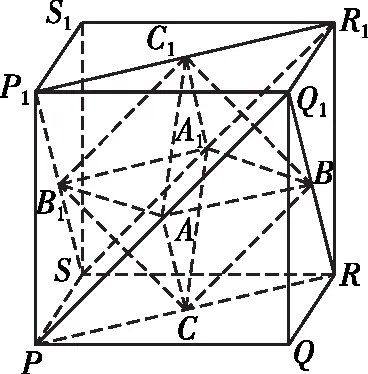
圖4

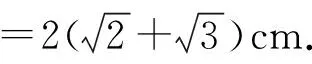
解法三:取BC的中點(diǎn)E,連接AE,A1E,過點(diǎn)A1作A1G⊥AE交AE的延長(zhǎng)線于點(diǎn)G,如圖5.

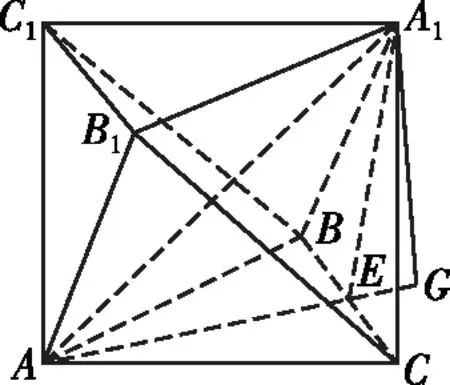
圖5

∵平面ABC∥平面A1B1C1,

∴兩平面的距離可化為點(diǎn)A1到平面ABC的距離,設(shè)為h.又∵正八面體ABC-A1B1C1是對(duì)稱的,∴A1G⊥平面ABC,

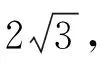
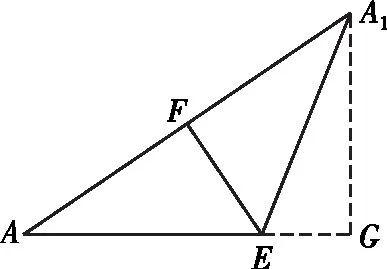
圖6

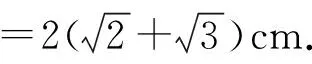
解法四:∵平面ABC∥平面A1B1C1,

∴兩平面的距離可化為點(diǎn)A1到平面ABC的距離,

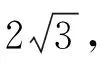
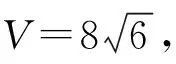
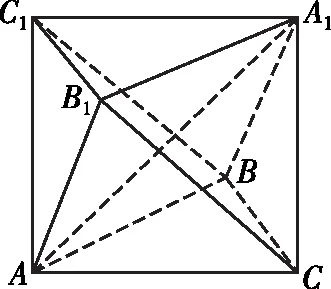
圖7

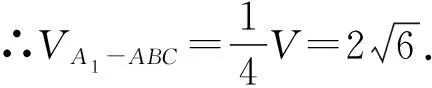
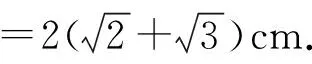
(本文系福建省教育科學(xué)“十四五”規(guī)劃2021年度立項(xiàng)課題《基于核心素養(yǎng)的高中數(shù)學(xué)探究性學(xué)習(xí)實(shí)踐與研究》課題編號(hào)(FJJKZX21-283)的階段性研究成果)