上海市民辦交大南洋中學(xué)(201504) 李麗娜

圓錐曲線是歷年高考試題的熱點(diǎn)問(wèn)題,其中客觀題主要考察離心率和雙曲線特有的漸近線的一些簡(jiǎn)單知識(shí),而主觀題經(jīng)常以壓軸題的形式出現(xiàn),考察知識(shí)全面,系統(tǒng),而且計(jì)算量比較大,得分比較困難.歷年高考?jí)狠S題中對(duì)圓錐曲線的考察大體可以歸納為如下四個(gè)部分:方程(軌跡)問(wèn)題,最值(取值范圍)問(wèn)題,定值(定點(diǎn))問(wèn)題,“是否存在”問(wèn)題.本文就定值問(wèn)題中的直接證明某個(gè)量為定值的問(wèn)題(不包含是否為定值的問(wèn)題)作點(diǎn)簡(jiǎn)單的說(shuō)明.在教學(xué)過(guò)程中,筆者常常聽(tīng)到學(xué)生說(shuō)“要是先知道定值是多少就好了?也好確定自己算的對(duì)不對(duì).”,下面通過(guò)幾個(gè)典型的高考?jí)狠S題,就如何通過(guò)一些特殊的方式先來(lái)確定‘定值’是多少,好做到心中有數(shù),淺談一下自己在教學(xué)過(guò)程中的做法.

例1 (2011四川理21)橢圓有兩定點(diǎn)A(-1,0),B(1,0),過(guò)其焦點(diǎn)F(1,0)的直線l與橢圓交于C,D兩點(diǎn),并與x軸交于點(diǎn)P.直線AC與直線BD交于點(diǎn)Q.

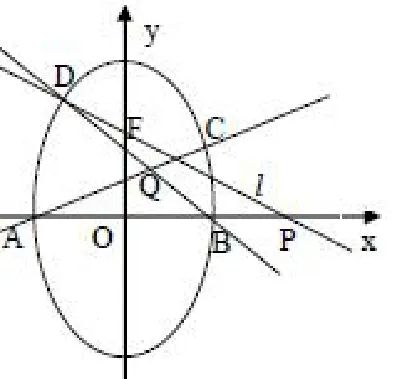
圖1

分析 主要分析下第(2)問(wèn):解決此類問(wèn)題一般是先通過(guò)題目中的一些特殊的點(diǎn),線位置關(guān)系來(lái)先確定定值是多少,然后再通過(guò)詳細(xì)的計(jì)算或推理加以嚴(yán)格的證明.點(diǎn)決定線的位置,于是解決問(wèn)題的關(guān)鍵就是先去尋找特殊的點(diǎn).特殊的點(diǎn)一般具有如下特征:比如圓錐曲線與坐標(biāo)軸的交點(diǎn),當(dāng)然點(diǎn)的選取首先要保證計(jì)算簡(jiǎn)單,如果選的點(diǎn)不當(dāng)?shù)脑?計(jì)算量會(huì)非常大,這就與我們最初的目的背道而馳了.

通過(guò)第二問(wèn)的題干,我們可以明顯的感覺(jué)到特殊的點(diǎn)應(yīng)該是A,B,為什么會(huì)有這樣的感覺(jué),那就是命題人為什么把這兩個(gè)點(diǎn)給排除了?是兩個(gè)點(diǎn)對(duì)于題干的設(shè)問(wèn)比較簡(jiǎn)單(易于計(jì)算),還是兩個(gè)點(diǎn)在題干所敘述的情況下沒(méi)有意義呢?下面我們來(lái)分析一下這兩個(gè)點(diǎn):

以點(diǎn)P與B重合為例:此時(shí)D點(diǎn)肯定不與B重合(如果重合,直線BD不存在),而C,Q與點(diǎn)B重合,可見(jiàn)此時(shí)這種情況在題干敘述的情況下是存在的,有意義的.我們很容易就可以得到這種情況下,這樣我們就得到了這個(gè)定值.

在大題中再通過(guò)推理或計(jì)算驗(yàn)證就可以了,如果在選擇或填空中出現(xiàn)這樣的題目,可以起到事倍功半的效果.

同理可以驗(yàn)證P與A重合的情況,在此不再多說(shuō).

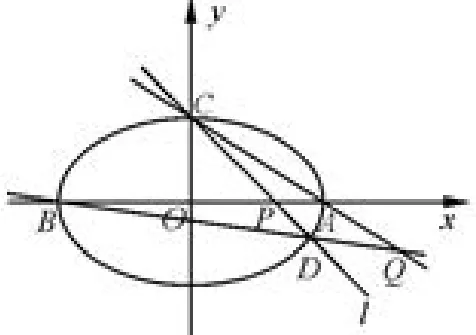
圖2

分析 通過(guò)題干P異于B點(diǎn),我們很明顯的可以感覺(jué)到此題中P與A點(diǎn)重合是可以的,可見(jiàn)這就是我們要尋找的特殊的位置關(guān)系,顯然此時(shí)D,Q與點(diǎn)A也重合了,只有這樣,題干所敘述的情況才會(huì)出現(xiàn).因此可以得到

上述兩個(gè)例題的詳細(xì)解法可以參考高考試題的參考答案所提供的解題過(guò)程.

(1)求橢圓C的方程;

(2)E,F是橢圓上C的兩個(gè)動(dòng)點(diǎn),如果直線AE的斜率與AF的斜率互為相反數(shù),證明:直線EF的斜率為定值,并求出這個(gè)定值.

分析 主要分析第(2)問(wèn):題干中的關(guān)鍵是直線AE的斜率與AF的斜率互為相反數(shù),這句話說(shuō)明直線AE,AF與x軸的交點(diǎn)和過(guò)點(diǎn)A,且與x軸垂直的直線是對(duì)稱的.此時(shí)可以考慮特殊的位置,讓點(diǎn)F與橢圓的右頂點(diǎn)重合,根據(jù)上述分析,結(jié)合橢圓的方程(半長(zhǎng)軸為4),(直線AE)必過(guò)原點(diǎn),根據(jù)對(duì)稱關(guān)系,可以求得E的坐標(biāo)為從而.此題的詳細(xì)解法可以參考高考試題的參考答案所提供的解題過(guò)程,下面提供此命題的一個(gè)推廣:

設(shè)A(x0,y0)是橢圓=1(a＞b＞0)上的一個(gè)定點(diǎn),E,F是橢圓上的兩個(gè)動(dòng)點(diǎn),如果直線AE的斜率與AF的斜率互為相反數(shù),證明:直線EF的斜率為定值,并求出這個(gè)定值.

我們還可以在雙曲線和拋物線中得到類似的結(jié)論,類似的題目在高考試題中還有2004年北京卷理科的17題和2005年江西卷文科的22題,此次不再說(shuō)明.

最后,顯然通過(guò)上述方法得到的定值需要進(jìn)行嚴(yán)格的證明,但在考試過(guò)程中可以讓學(xué)生做到心中有數(shù),來(lái)確定自己最后的計(jì)算是否正確.在選擇或填空中,通過(guò)點(diǎn)的特殊的位置關(guān)系來(lái)確定定值,可以節(jié)約考試時(shí)間,起到很好的效果.類似的題目在高考中還是比較多的,比如2007年重慶理科的壓軸題.